设计仿真 | 基于开裂能量密度方法的橡胶件疲劳寿命分析

在橡胶件CAE仿真分析中，橡胶件刚度，密封性等仿真工况的分析相对容易，但是如何进行橡胶疲劳寿命的分析当前还是困扰工程师的一个难题。

Marc在橡胶、密封行业有着广泛的应用，针对橡胶疲劳寿命的仿真，Marc有几种方法可以实现：

01  Mullins效应

❖ 通过Mullins效应进行橡胶件的损伤分析，当损伤到达1时，认为橡胶出现开裂，但是在实际仿真计算中需要进行大量的分析计算，工作量巨大。

02  弹性体疲劳寿命损伤理论

❖通过弹性体疲劳寿命损伤理论来进行疲劳寿命分析，基本思想和传统的金属疲劳的一致，仿真计算工作量很小，适合在工程计算中应用。

03  基于开裂能量密度

❖ 通过开裂能量密度的方法进行疲劳寿命的计算，基于裂纹扩展的基本假设，考虑拉伸载荷作用和平均应力的修正，并给出关键区域的开裂方向。相对于上面的方法，其分析精度较高。

开裂能密度理论介绍    

基于开裂能量密度(CED)的弹性体方法属于裂纹扩展方法的范畴，该方法假设材料中总是存在小裂纹，例如尺寸为c₀，并且由于循环载荷，它们会生长，直到达到材料被认为失效的尺寸。假设初始裂纹尺寸c₀是材料的特征参数，由于循环载荷，这些裂纹不断扩展，直到达到材料失效的尺寸c_f。裂纹扩展速率r具有幂律的形式：

裂纹扩展速率被定义为每循环次数变化的裂纹尺寸变化dc/dN。其中，T_max是加载循环中的最大能量释放率（撕裂能量）。T_c是立即发生断裂的T_max的临界值，r_c是对应于T_c的最大裂纹扩展速率。裂纹寿命计算表达式如下：

假设小裂纹的能量释放率与裂纹的尺寸c成比例，如下所示：

同时，最大的能量释放率可以表达为如下形式：

可得出，疲劳寿命的计算公式如下：

应该要指出的是，裂纹能量密度不仅取决于应力和应变状态，还取决于假定裂纹平面的方向。因此，在实际计算中需要进行关键平面搜索，以评估使疲劳寿命最小化的方向。

橡胶体疲劳案例介绍    

以橡胶件，衬套为例，首先在现有的橡胶材料模型参数的参数基础上，需增加用于弹性体疲劳计算的参数，如下图所示：

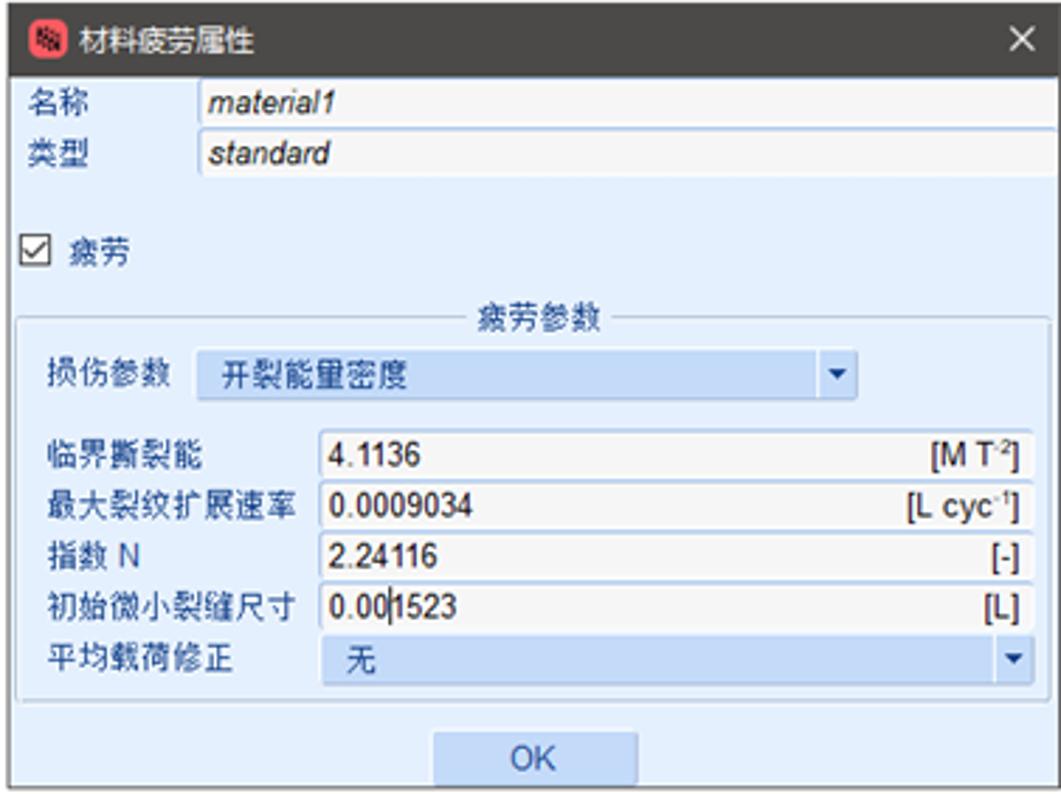
其中，系数W_max、r_c、N、c₀、分别为临界撕裂能量，最大裂纹扩展速率，指数系数，初始微裂纹尺寸。模型计算时不考虑载荷比值的修正。其次，定义橡胶衬套的载荷计算工况。在该案例中，我们先约束衬套的中心和对称面，同时定义衬套的边缘沿径向和轴向同时加载1mm的正弦振动。载荷加载形式为正弦波，在一个正则时间步内完成。

同时在结果输出中，需要将柯西应力张量和应变梯度进行输出，以用于后续的疲劳寿命计算。计算结果如下图所示。可以看到，最大对数主应变发生在橡胶衬套和套筒的接触位置已经在衬套边缘特征位置。

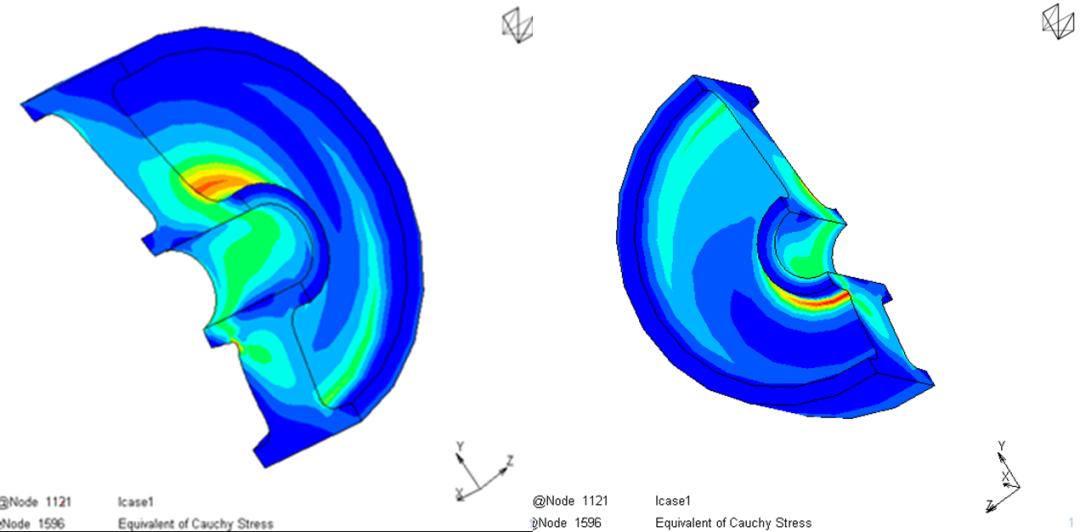
在此基础上，新增一个用于疲劳计算的分析任务，用于疲劳寿命计算。其计算设定参数如下图所示。其中，载荷类型采用变幅载荷，并选定前一步计算好的结果文件。定义好寿命计算的增量步范畴，该分析取第一步到最后一步的应变进行疲劳寿命计算。

疲劳计算结果如下图所示，可以看到其损伤最大的位置在橡胶特征倒角处，最小对数寿命为2.7。这与前面计算的最大等效柯西应力位置对应。同时，还可以预测出橡胶裂纹开裂面，如下图所示。其中红色箭头所指的方向即为疲劳开裂平面的法向。

小 结

与基于马林斯效应和基于应变寿命曲线的弹性体疲劳相比，基于开裂能量密度的方法，可以更加精确的进行橡胶件的疲劳寿命预测和开裂方向预测。

采用Marc软件，可以很方便的在计算完强度的基础上，进行橡胶件疲劳寿命的计算。从而帮助客户快速预测橡胶件的疲劳寿命，提升产品开发效率。

（海克斯康工业软件）

声明：本网站所收集的部分公开资料来源于互联网，转载的目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传，对此类作品本站仅提供交流平台，不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题，请第一时间告知，我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容，以保证您的权益！联系电话：010-58612588 或 Email:editor@mmsonline.com.cn。