原创 | 短圆柱大平面垂直度问题讨论
一、问题
如下图所示简化图纸,一个大平面和短圆柱轴线评价垂直度:
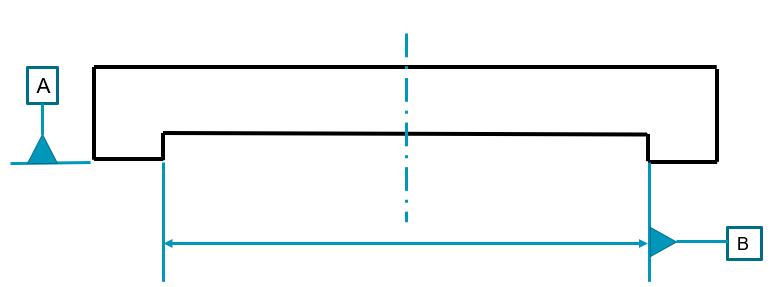
以平面为基准评价圆柱轴线的垂直度结果是0.002;
以圆柱轴线为基准评价平面的垂直度结果是0.106;
为何会有如此大的差距呢?
二、两种评价方式算法差异
两种评价方式结果不同是垂直度算法使然。
(1)以平面为基准评价圆柱轴线垂直度,公差带形状是垂直于基准平面的圆柱,该圆柱需要将被评价的轴线完全包裹,所需的最小圆柱直径就是垂直度结果。
为了便于说明,我们假定平面和圆柱轴线都是没有形状误差的,二者只是有一定的倾斜角度,如下所示的简化图——蓝色线代表大平面、绿色线代表短圆柱轴线。

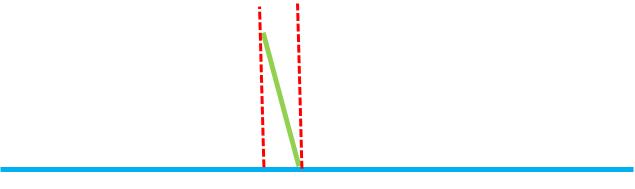
如下简化图所示以平面为基准评价圆柱轴线垂直度,公差带是垂直于蓝色平面的圆柱在下图用红色虚线表示,红色虚线完全包裹绿色圆柱轴线,两红色虚线之间的距离就是垂直度结果。

由此也可以看出,在二者夹角相同的情况下圆柱轴线越长,垂直度结果越大,如下图简化示意图所示。
(2)以圆柱轴线为基准评价平面垂直度,公差带是垂直于圆柱轴线的两个平行平面,平行平面需要将被评价的平面完全包裹,包裹所需的间距最小的平行平面的间距就是垂直度结果。
还是以(1)中没有形状误差的蓝色大平面和绿色线短圆柱轴线来计算,公差带的形状是垂直于圆柱轴线的两个平行平面用红色虚线表示,红色虚线完全包裹住蓝色平面,两红色虚线之间的距离就是垂直度结果。
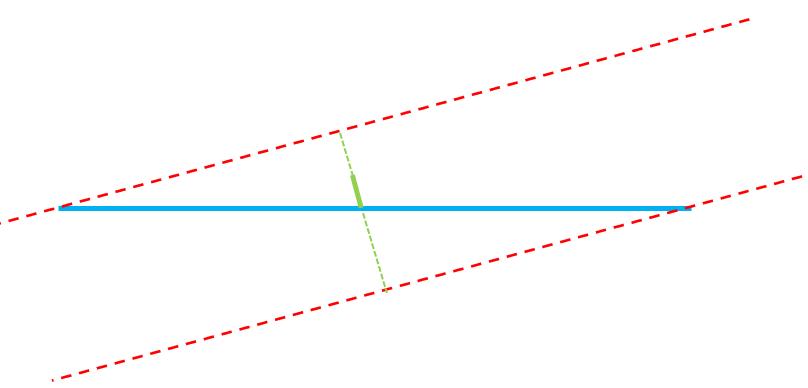
同样的,在二者夹角相同的情况下平面越大,垂直度结果也越大。
再来对比一下以平面为基准评价圆柱轴线的垂直度的示意图,可以看到虽然是同一组平面和圆柱轴线二者夹角相同,但是两种评价方式的结果有着很大的差距。

三、短圆柱的测量不确定性
假定一种情况:圆柱轴线是由Z坐标不同的两层圆的圆心连线构造成的,并且两层圆心在投影到XY 平面上的距离相等,那么如图所示两层圆的Z坐标相距越远即圆柱轴线越长,圆柱轴线的倾斜越小。
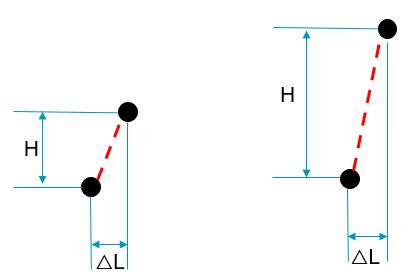
左右两张图,△L相同,但是右边H是左边H的2倍,可以很明显的看到右侧直线的倾斜角度比左边小。
我们可以假定这个△L为每次测量的测量误差(实际测量中没有这么大误差,为方便叙述夸张误差),由于H较小导致圆柱轴线的倾斜变化量很大,造成以圆柱轴线为基准评价平面垂直度的公差带变化量很大,造成结果不稳定如下所示示意图。
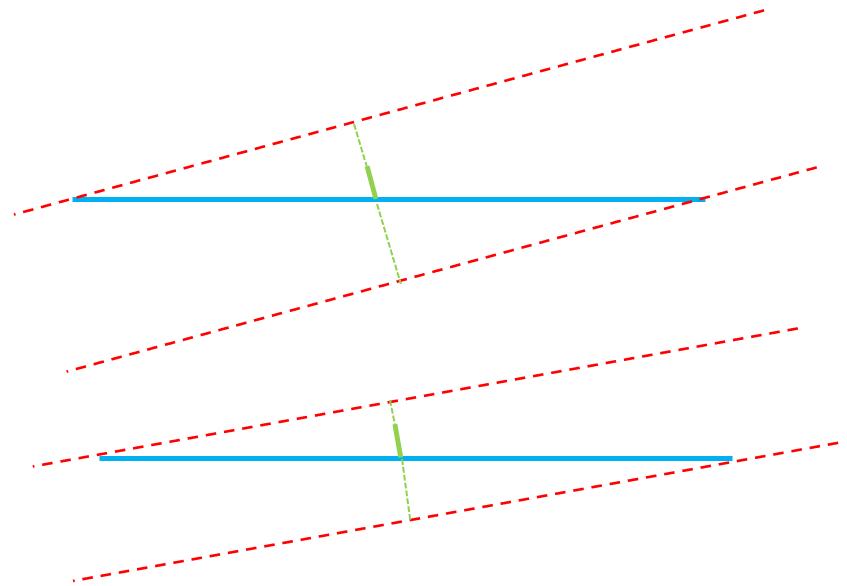
由图可看到,绿色轴线角度倾斜一点评价结果就差距很大,并且已知短圆柱测量容易造成倾斜不稳定的情况,由此可以看出以短圆柱轴线评价大平面的垂直度测量结果相对不稳定。
四、数学计算分析
我们仍然假定平面和圆柱轴线都是没有形状误差的,然后通过计算得到不同情况下的垂直度结果。
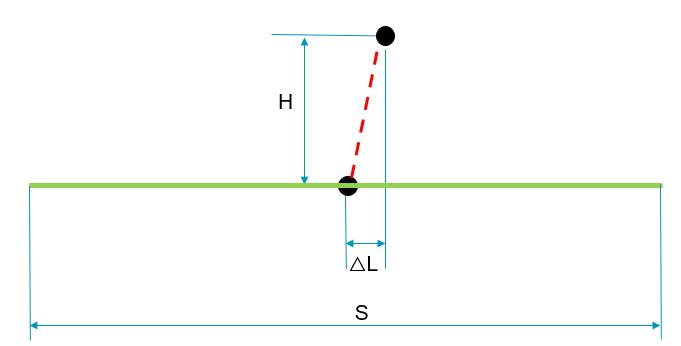
一共三个参数:
H——圆柱轴线的长度;
△L——两层圆心投影到理论平面上的距离;
S——平面长度;
先假设H=3㎜,△L=0.01㎜,S=200㎜
二者夹角α=arctan(H/△L)= arctan(3/0.01)=89.8090°
以圆柱轴线为基准评价平面的垂直度结果T=S·sin(90-α)=200×sin(90-89.8090)=0.6667;
以平面为基准评价圆柱轴线的垂直度结果T=H·tan(90-α)=3× tan(90-89.8090)=0.01,从图中也可以看出结果就是△L;
再计算几组数据结果汇总如下表:
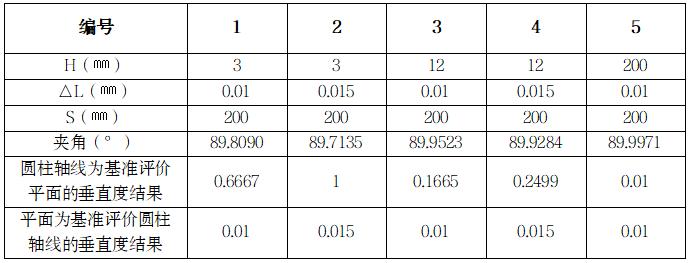
●对比1和2可以看到在H是3㎜的时候,△L从0.01㎜变化到0.015㎜时,以圆柱轴线为基准评价平面的垂直度结果从0.6667㎜变化到1㎜,变化量是0.3333㎜;
●对比3和4可以看到在H是12㎜的时候,△L从0.01㎜变化到0.015㎜时,以圆柱轴线为基准评价平面的垂直度结果从0.1665㎜变化到0.2499㎜,变化量是0.0834㎜;
由此可以看出以短圆柱轴线为基准评价平面的垂直度结果不稳定。
●对比1和3可以看到,仅仅是H发生变化以圆柱轴线为基准评价平面的垂直度结果变化很大;
●结合5可以看到,只有H和S都是200时,以圆柱轴线为基准评价平面的垂直度结果和以平面为基准评价圆柱轴线的垂直度结果相等。
五、综述
以上情况分析为了方便叙述假定了没有形状偏差的平面和圆柱轴线,实际情况中要考虑圆柱轴线的直线度和平面的平面度的影响,但是不妨碍使用无形状偏差的平面和圆柱轴线进行情况说明和理解。
综合以上分析可以总结如下:
●以平面为基准评价圆柱轴线的垂直度和以圆柱轴线为基准评价平面的垂直度,两者结果有差异是垂直度算法问题的正常现象;
●短圆柱轴线作为基准评价大平面垂直度存在评价结果偏差较大并且评价结果相对不稳定的现象。
钜惠 · 推荐
热门 · 推荐
(陈伟 海克斯康育人平台)
声明:本网站所收集的部分公开资料来源于互联网,转载的目的在于传递更多信息及用于网络分享,并不代表本站赞同其观点和对其真实性负责,也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传,对此类作品本站仅提供交流平台,不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题,请第一时间告知,我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容,以保证您的权益!联系电话:010-58612588 或 Email:editor@mmsonline.com.cn。

- 暂无反馈







