海克斯康工业软件设计仿真 | 约束的代数方程

01 简 介

约束作为多体动力学的基本要素，应用在每个模型中。本文对软件界面的约束及其对应的代数方程进行整理说明，以期更好的应用软件。

约束可以分为定常约束（与时间无关的）和非定常约束（与时间相关的）。又可以分为完整约束（对位移进行约束）和非完整约束（对速度进行约束）。不同的分类应用在不同的分析场景，本文只对空间定常约束，即大家熟悉的固定副、球副、圆柱副、移动副、旋转副、万向副、平行副、垂直副进行说明。

02约束的代数方程

固定副

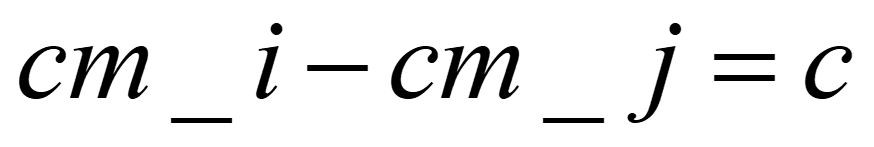
即部件j的质心与部件i的质心位置/角度的差值是个常数。

球副

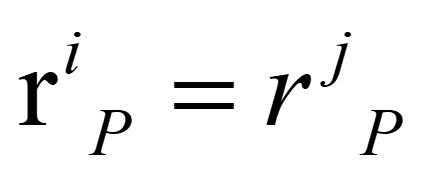
全局坐标系下，部件i与部件j的这两个点位置始终重合，从而使部件j不能与部件i有相对运动，即限制了部件j的三个移动自由度。

圆柱副

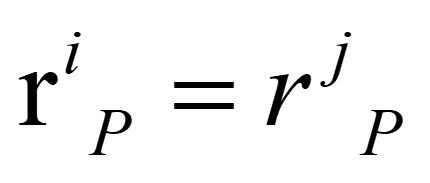
第一项，部件i与部件j上的两个向量一直平行，限制了部件j绕部件i两个方向的转动（若是部件j能够相对转动，那么初始平行的两个向量就不满足平行关系）；第二项，部件i上的向量与约束轴线平行，限制了部件j的两个移动（若是部件j朝着其他方向移动，那么s^ij与hⁱ将不再平行）。

移动副

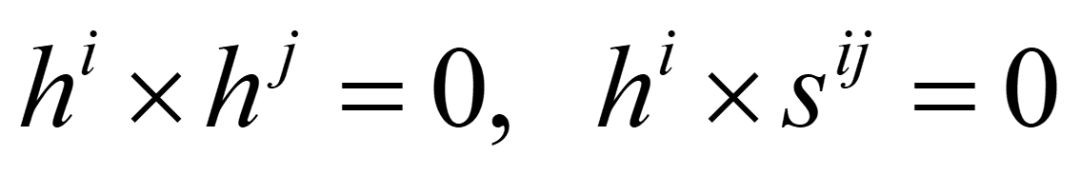
在圆柱副的基础上再加第三项，额外限制旋转，nⁱ与n^j分别是在部件i与部件j上的两个向量，相互垂直，且都垂直于约束轴线。（若是部件j转动，那么两个向量将不满足垂直关系）

旋转副

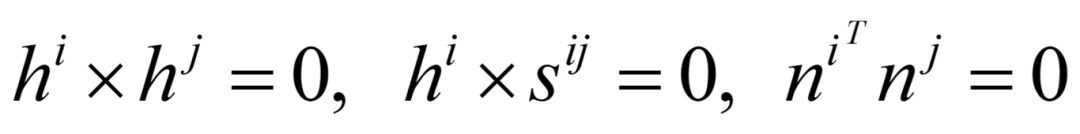
在圆柱副的基础上再加第三项，额外限制移动，及s^ij在这个方向的投影一直是0，或者一个常数。

万向副

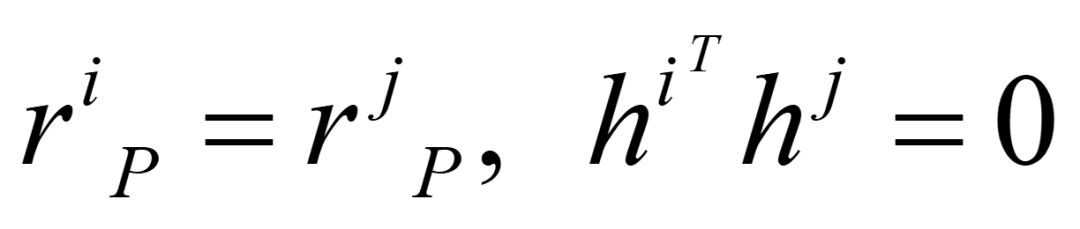
球副的基础上再额外限制旋转。（道理同移动副的第三项）

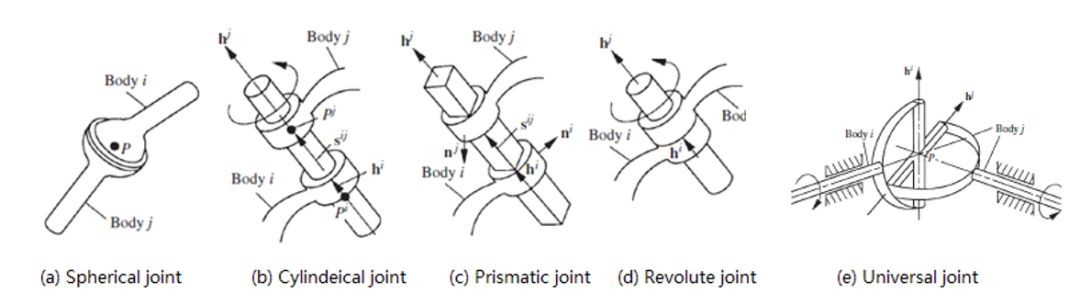
图1 常见约束副

表1 约束公式汇总

从上表也可以看出，旋转副也可以用一个球副叠加限制两个旋转自由度的平行副：

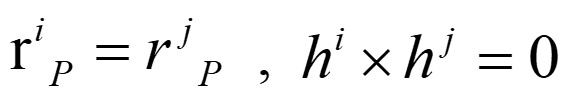
也可以看出垂直副、平行副是基础副，其他约束可以用其来构造。

03 万向副的验证

万向副由于其约束关系，存在不等速的特性。本节通过Matlab与Adams分别建立模型，验证此特性。

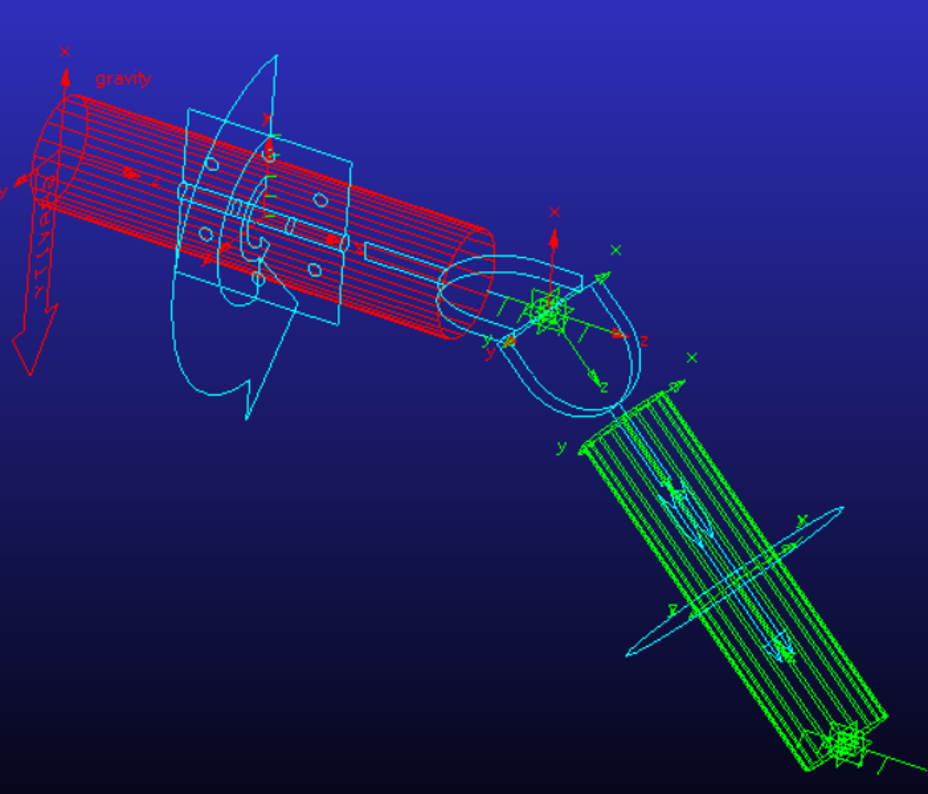
图2 万向副验证模型

在Adams中创建部件i（红色圆柱），部件j（绿色圆柱），部件i与大地旋转副约束，并施加60deg/s的恒定角速度驱动；部件j与大地平行副约束，部件j与部件i万向副约束。

在Matlab中，采用相同的约束。

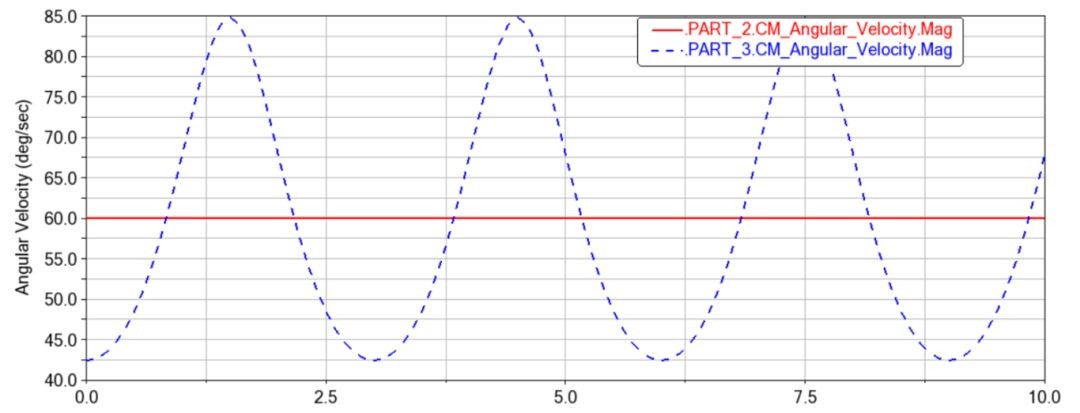
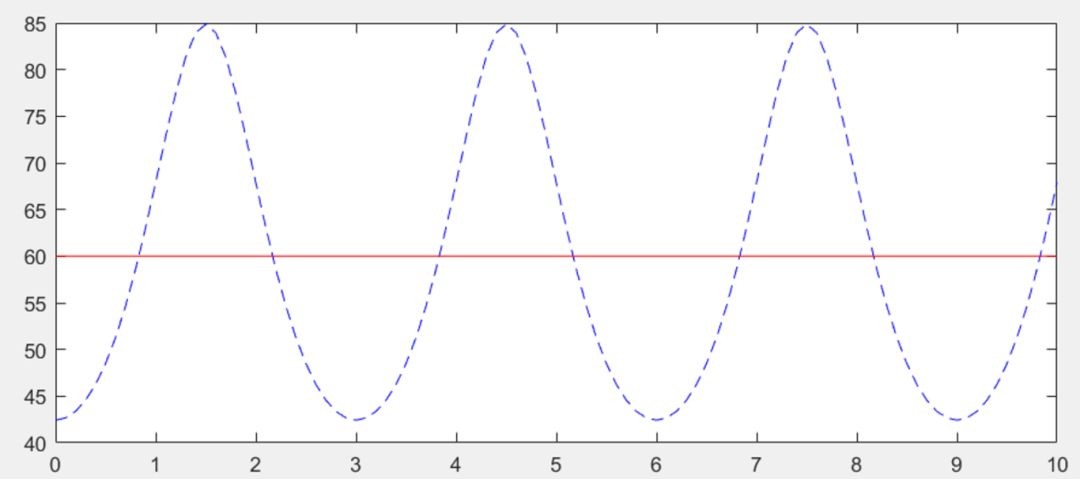
图3 Adams结果VS Matlab结果

两者结果完全一样，验证了上述旋转副、万向副及平行副的代数方程。

04 参考文献

[1] computational Dynamics (3rd). Ahmed A. Shabana.

（海克斯康工业软件）

声明：本网站所收集的部分公开资料来源于互联网，转载的目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传，对此类作品本站仅提供交流平台，不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题，请第一时间告知，我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容，以保证您的权益！联系电话：010-58612588 或 Email:editor@mmsonline.com.cn。