参数自调模糊控制方法在机器人中的应用（2）

四、模糊控制规则

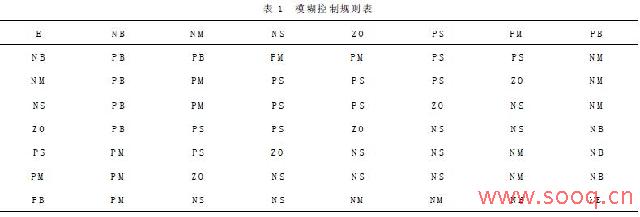
通常情况下模糊控制规则是由实际的控制经验总结出来的，但对于船体表面清刷机器人这种在特定环境中作业的控制对象，要总结出人工控制经验是较为困难的。可以从系统简化的物理模型出发，按常规控制经验类推出一般的模糊推理规则;也可以将经典控制理论模糊化得到一套相应的模糊控制规则去控制机器人在船体表面的移动。采用的模糊控制规则为

Ri:if E is Ai and EC is Bi，then △U is Ci

    其中Ri 表示第i条控制规则；E表示误差语言变量；EC表示误差变化率语言变量；△U 为控制量语言变量。

    它们的语言值在相应论域中的模糊子集分别为Ai，Bi和Ci，由这些控制规则可得到模糊控制规则表1。

 五、量化因子、比例因子和参数自调整

采用计算机实现模糊控制算法进行模糊控制时，必须将采样得到的输入变量从基本论域转换到相应的模糊集的论域，因此，需要引入量化因子进行论域的变换。图2中的参数 K1和K2分别为误差的量化因子和误差变化率的量化因子。

每次采样经模糊控制算法给出的控制量(精确量)，还不能直接去控制对象，必须转换到控制对象所能接受的基本论域中去，即通过图（2）中的比例因子K3实现输出控制量的论域的变换。

由图（2）可知，模糊控制器除了要有一个好的模糊控制规则外，合理地选择模糊控制器输入变量的量化因子和输出控制量的比例因子也是非常重要的。研究表明，量化因子和比例因子的大小及不同量化因子之间大小的相对关系，对模糊控制器的控制性能影响极大。为了使清刷机器人能够适应各种不同船体表面上运动，完成规定的清刷功能，控制中采用的量化因子和比例因子可根据误差e和误差变化率e_c的大小进行自动调整，从而使系统在各种情况下都具有良好的控制性能。

量化因子K1和K2的大小对控制系统的动态性能影响很大。当e和e_c较大时，控制系统要减小误差，加快动态过程，这时应取较大的控制量。此时可缩小量化因子K1和K2，增大K3。当e和e_c较小是，系统接近稳定值，这时为了使稳态误差尽可能减小，应当放大量化因子K1和K2，同时减小K3，使控制量的阶跃变化小。

由以上分析可知，K1，K2和K3的变化趋势正好相反。为了便于计数机控制，可取K1，K2的变化倍数与K3的变化倍数成倒数关系。K1，K2和K3的调整也是采用模糊化方法，经模糊推理后得到参数调整表2。实际控制时，一最初设定的量化因子K10和K20对误差e和误差变化率ec进行量化，查找参数调整表得到N值，按K1=N·K10，K2=N·K20和K3=K30/N调整参数，开用调整后的K1，K2和K3进行量化和控制。 

声明：本网站所收集的部分公开资料来源于互联网，转载的目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传，对此类作品本站仅提供交流平台，不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题，请第一时间告知，我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容，以保证您的权益！联系电话：010-58612588 或 Email:editor@mmsonline.com.cn。