大圆弧上中心线相交斜孔的加工方法
1. 提出问题
在生产过程中会遇到这样的零件,如图1所示,该零件外形尺寸小且在圆弧上均布5个φ25H9孔,各孔中心又与圆弧中心交于同一点。如何既简单又方便地加工这些斜孔并保证精度成为一个棘手的问题。
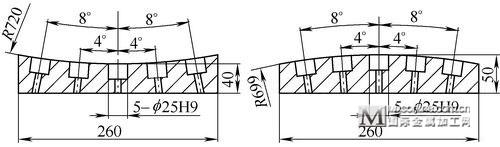
图 1
2. 分析问题
按传统工艺方案有三种加工方法:①划线法,划出各孔位置,按线加工孔。但是由于圆弧半径大,划线困难,精度难以保证。②放置零件使其圆弧中心与工作台旋转中心重合,旋转工作台加工孔。但此种方法需要选用大规格机床(即工作台回转半径必须大于圆弧半径),并且要使两中心完全重合,操作难度极大。③利用五轴数控机床加工,这种方法简单且容易操作。但受机床限制,若无五轴机床就无法加工,并且加工成本高。如何在常规机床上加工出此类零件就成了一个迫切需要解决的问题。
零件在工作台任意位置放置,我们要求零件的直边与机床主轴垂直,然后夹紧,零件随工作台一起旋转,故旋转后要加工的孔将不在主轴正下方,其孔的中心和主轴中心在X轴方向将产生一段距离,工作台沿X轴方向补偿此段距离后,方能加工该孔,因此确定该补偿的距离成了难点。
3. 解决问题
(1)作图法确定补偿距离 利用AutoCAD软件在计算机上模拟画出工作台及旋转中心位置,再根据装夹位置(装夹时使零件的直边与机床主轴垂直)测量出A、B值,画出零件在工作台上的准确位置,如图2所示,工作台补偿距离A,即可加工中间孔。
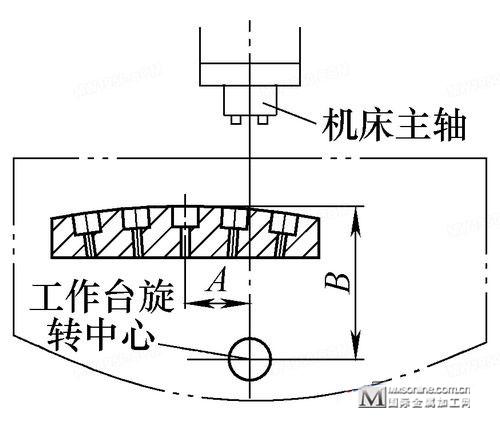
图2
工作台按图样顺时针旋转4°,如图3所示,测量出X1值,实际加工中工作台沿X轴方向补偿距离X1,即可加工4°位置孔。
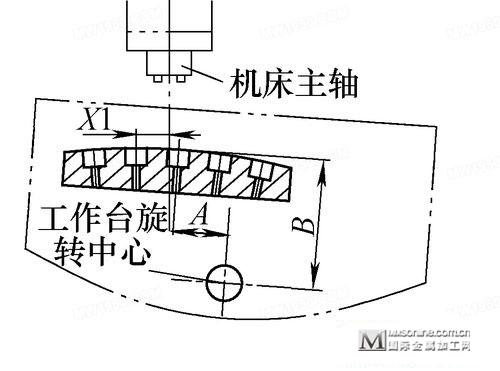
图3
工作台按顺时针旋转8°,如图4所示,测量出X2值,实际加工中工作台沿X轴方向补偿距离X2,即可加工8°位置孔。
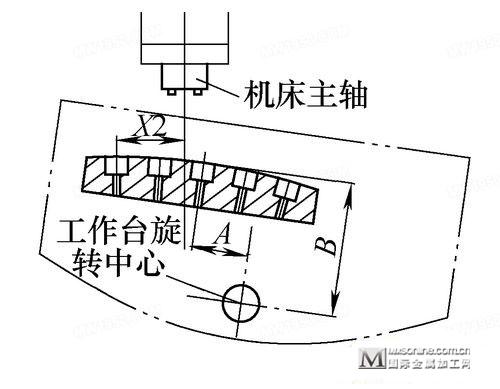
图4
逆时针方向4°、8°孔的位置按同样方法得出X,即可加工。
(2)计算法确定补偿距离 以凹圆弧为例,工作台顺时针旋转β角,如图5所示,直角三角形3和直角三角形2全等,三角形3中已知一直角边为A,夹角为β/2,另一直角边通过Atan(β/2)求出;直角三角形1中,角度β已知,斜边为R、B及三角形3一直角边三段之和,由此即可求解出X。
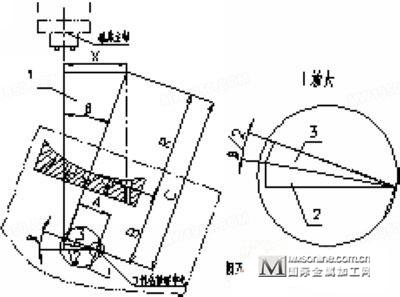
图 5
工作台顺时针旋转β后工作台沿X轴方向补偿距离的计算公式为
X=[C+Atan(β/2)]sinβ,其中C=R+B
工作台逆时针旋转β后工作台沿X轴方向补偿距离的计算公式为
X=[C-Atan(β/2)]sinβ,其中C=R+B
凸圆弧与凹圆弧计算方法相同,在此不再赘述,只给出计算公式。
工作台顺时针旋转β后工作台沿X轴方向补偿距离的计算公式为
X=[C+Atan(β/2)]sinβ,其中C=R-B
工作台逆时针旋转β后工作台沿X轴方向补偿距离的计算公式为
X=[C-Atan(β/2)]sinβ,其中C=R-B
4. 结语
由于A、B值是作图或计算的基本数据,因此必须精确测量该值,可采用在工作台旋转中心定位孔内装检套检棒进行测量。为了精确测量A、B值,零件外形采用精铣加工,各面平行垂直控制在0.02mm内,外形及R圆弧表面粗糙度值Ra≤1.6mm。
采用以上所述方法,在我公司的TH6350卧式加工中心(工作台500mm×500mm)上成功加工出此零件,经过检验其精度满足设计要求,证明此方法经济、简单、可靠,值得推广。
声明:本网站所收集的部分公开资料来源于互联网,转载的目的在于传递更多信息及用于网络分享,并不代表本站赞同其观点和对其真实性负责,也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传,对此类作品本站仅提供交流平台,不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题,请第一时间告知,我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容,以保证您的权益!联系电话:010-58612588 或 Email:editor@mmsonline.com.cn。

雷尼绍参展慕尼黑上海光博会2025
- 暂无反馈
