局部旋转惯性对航空燃气轮机转子系统动力特性的影响
提出了基于质心和惯性主轴空间位置的转子旋转惯性描述方法,推导了旋转惯性载荷在不同运动状态下的完整表达式,建立了考虑轮盘质心横向运动和惯性主轴角向运动的连续梁转子模型及运动微分方程。分析表明:高转速下轮盘具有“质心自动定心”与“惯性主轴自动掰正”的趋势,这种旋转惯性将提高转子系统正进动模态频率,并增大转子支点动载荷,盘⁃轴连接局部角向刚度是决定其影响程度的关键。在此基础上,解释了高转速下转子支点动载荷随转速提高而持续增大的原因,探究了盘⁃轴连接局部角向刚度对转子系统固有特性和动力学响应的影响规律,为高转速复杂结构转子动力学设计与振动故障排查,提供了理论支撑。
关键词 旋转惯性;非连续性;惯性主轴;动力特性;自动定心
转子⁃支承结构系统是航空燃气轮机等旋转机械的核心结构系统,也是主要的振动激励源。其中,旋转状态下由于转子质量分布不均匀而产生的旋转惯性载荷,则是转子中※常见和※主要的激励形式,此激励同时也是其他激励(如转静子碰摩激励等)的直接或间接产生原因。
旋转惯性载荷,是指转子旋转时,各质点做非惯性运动,动量与角动量时刻发生改变,由于运动惯性的存在,所受到的阻止其运动状态发生改变的阻抗载荷,常见的表现形式有:不平衡力、陀螺力矩等。
随着航空燃气轮机技术持续发展,转子工作转速不断提高,跨越多阶临界转速,尤其是弯曲振型临界转速(下简称弯曲临界),在这一过程中,国内外学者与工程师对转子旋转惯性载荷的认识也在逐步深入,随之体现在转子设计理念与平衡技术的进步中。
1919年,Jeffcott[1]提出“Jeffcott转子”模型,即刚性轮盘居中的无重轴转子模型,首次指出转子质心与形心的偏离,所引起的旋转惯性载荷,是转子产生涡动的主要原因,这是认识转子动力学行为的重要进步[2]。1933年,Smith[3]在“Jeffcott转子”模型的基础上,推导了同时具有横向与角向自由度的刚性转子运动方程,并分析了轮盘质心偏移和惯性主轴倾斜引起的转子动力学响应,一般称为“四自由度转子”模型。众多学者,如Den Hartog、Timoshenko[4⁃5]先后完善了“四自由度转子”模型理论。
至此,刚性转子旋转惯性的理论研究已趋于完善,学者与工程师对刚体临界转速附近的转子旋转惯性载荷与动力学行为,已经具备了较好的认识,此时恰逢航空燃气轮机首次投入使用,功率不高、转速较低,设计师普遍依照“刚性转子”的理念开展转子结构设计,保证压气机/涡轮转子各自发生刚体位移。刚性转子的理论研究成果成功应用于当时的转子动力学设计中,国际公认的ISO1940平衡标准也应运而生,为工程实践中刚性转子的平稳工作提供理论支撑与方法指导。
20世纪后半叶,航空燃气轮机技术水平不断进步,要求更高的转子转速,多转子构形与多级压气机/涡轮的广泛应用,导致转子跨距不断加长,工作转速与弯曲临界不断靠近,转子的弯曲变形不可忽略,转子质量发生重新分布,旋转惯性载荷随之改变,此时即便刚性较好的高压转子,也按照“准刚性转子”理念开展设计。转子动力学中有关旋转惯性的研究,转向了柔性转子平衡方法,着重研究工作在弯曲临界以上的高速转子,发生弯曲变形后的质量分布及旋转惯性载荷的变化规律,在此基础上提出了相应的工程平衡方法。代表成果有:模态平衡法(包括N+2面法[6]、N面法[7])和影响系数法[8],随着研究的深入,相关平衡方法已纳入国际标准ISO 21940⁃12,较好地满足了当时航空燃气轮机柔性转子的振动控制需求。典型案例如,1979年,美国国家航空航天局(NASA)组织开展了影响系数法在T700发动机动力涡轮转子(※大转速为22 000 r/min)平衡中的应用,试验结果表明:柔性转子平衡方法可有效抑制多个工作转速下的转子振动,同时大幅精简了转子系统平衡流程,增强了T700发动机的外场维护性[9]。
进入21世纪,为提高航空燃气轮机的推重比/功重比,转子大量采用薄壁结构与新构形设计,转子系统“低弯曲刚度”与“高工作转速”的冲突持续加深,转子弯曲变形不断增大,愈发影响转子旋转惯性载荷及动力学响应。刘书国等[10]在法兰⁃螺栓转子系统的多周期试验中,发现了随工作周期累积的转子振幅增大现象,其原因是螺栓连接结构界面接触状态变化与损伤导致的转子不平衡量加大;陈雪骑等[11]通过仿真计算初步解释了转子界面接触状态变化引起附加不平衡量的内在机理。刘意等[12⁃14]以地面燃气轮机转子系统为研究对象,发现界面缺陷与界面平行误差等会导致轮盘质心随转速增大而持续偏离形心,由此引起的旋转惯性激励及转子振动响应也随之增大。
然而,现有的旋转惯性载荷研究,不能较好地支撑现代先进航空燃气轮机转子设计,体现在以下两方面:
1) 对复杂转子质量分布的描述,仍采用基于不平衡量(即质心偏移)轴向分布的描述方法,无法完备描述轮盘等转子组件的质量分布,及其旋转惯性和转子动力学响应;
2) 现代航空燃气轮机转子结构变形的一大特点为:轮盘与转轴的“角向位移非连续性”较强,主要是源于连接结构和几何构形突变处的角向位移阶跃,因此传统的转子动力学理论分析方法[15⁃16]的“角向位移连续性”假设——轮盘与转轴是刚性连接,即轮盘与转轴的横向位移相等,轮盘角向位移等于转轴横向变形的偏导数。这一假设从本质上讲,使轮盘的横向与角向运动完全从属于转轴的横向运动,已不再适用于现代航空燃气轮机转子系统。为此,本文将建立完整的转子旋转惯性载荷力学模型,建立考虑“盘⁃轴角向位移非连续性”的转子动力学理论模型与方程,探究“盘⁃轴角向位移非连续性”对转子动力学响应的影响,为高速转子结构系统的动力学设计提供理论分析方法。
1 角向位移非连续性
现代先进航空燃气轮机转子设计中,大量采用不同材料、不同几何构形的结构,并通过多种类型的连接结构完成装配,转子结构具有较强的“结构特征非连续性”,主要表现为:连接结构处的接触状态非连续,与几何突变处的截面尺寸非连续,如图1所示。

图1 航空燃气轮机转子结构特征非连续性示意图
Fig.1 Schematic diagram of non⁃continuity of rotor structural characteristics in aircraft gas turbine engines
工作状态下转子发生较大弯曲变形时,将导致大质量/转动惯量轮盘局部的“盘⁃轴角向位移非连续性”,如图2所示,主要体现在:①经过多个工作循环后,连接结构配合界面可能发生不可恢复变形,界面接触状态和应力分布产生突变、阶跃特性,导致连接结构局部存在角向位移突变 
![]() ;②几何突变处(如盘⁃轴几何突变)即使采用焊接或一体化加工,连接处可以保证位移连续性,但由于局部连接角向刚度较弱,几何突变处的弯曲变形梯度过大,宏观来看,轮盘整体不再垂直于转轴弹性线切线,即轮盘角向位移与该处轴段角向位移存在差值
;②几何突变处(如盘⁃轴几何突变)即使采用焊接或一体化加工,连接处可以保证位移连续性,但由于局部连接角向刚度较弱,几何突变处的弯曲变形梯度过大,宏观来看,轮盘整体不再垂直于转轴弹性线切线,即轮盘角向位移与该处轴段角向位移存在差值 ![]() 。
。

图2 转子结构的角向位移非连续性示意图Fig.2 Schematic diagram of non⁃continuity of angular displacement in rotor structures高转速状态下,“盘⁃轴角向位移非连续性”将使得轮盘在横向与角向自由度上的旋转运动独立于转轴横向运动,由此将改变轮盘的旋转惯性载荷,进一步影响转轴的横向动力学响应,尤其是支点动载荷。
2 旋转惯性载荷力学模型
旋转惯性载荷,是非惯性坐标系中的惯性力在转子动力学中的具体体现。旋转惯性载荷大小等于其动量与角动量的变化速率,方向与其变化量方向相反,如式(1)所示
| (1) |
式中 
![]() 是旋转惯性力,
是旋转惯性力, 
![]() 是旋转惯性力矩,
是旋转惯性力矩, 
![]() 是转子动量,
是转子动量, 
![]() 是转子角动量。本文以轮盘为研究对象,重新梳理旋转惯性载荷的一般性表达式,以阐释其物理内涵。
是转子角动量。本文以轮盘为研究对象,重新梳理旋转惯性载荷的一般性表达式,以阐释其物理内涵。
2.1 转子旋转惯性描述方法
轮盘的运动状态由其动量与角动量完全确定,因此可通过其质量分布特性与运动速度完整描述[17]。由于其径向高度与轴向尺寸均较大,整体刚性较好,在高速转动时仍可近似视作刚体。轮盘动量为各质点动量之和,如下:
| (2) |
式中 
![]() 是质点线速度矢量,
是质点线速度矢量, 
![]() 是质点的质量,
是质点的质量, 
![]() 是质点的位置矢量,
是质点的位置矢量, 
![]() 是轮盘质心G的位置矢量,dm为轮盘中微元体的质量。轮盘的角动量为各质点动量对参考轴的主矩之和,如图3所示。
是轮盘质心G的位置矢量,dm为轮盘中微元体的质量。轮盘的角动量为各质点动量对参考轴的主矩之和,如图3所示。
| (3) |
式中 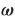
![]() 为轮盘的角速度矢量,
为轮盘的角速度矢量, 
![]() 是轮盘的转动惯量矩阵,一般定义式如下:
是轮盘的转动惯量矩阵,一般定义式如下:
| (4) |
式中x、y、z分别为微元体的坐标。

图3 轮盘运动示意图Fig.3 Schematic diagram of spinning disk由式(4)可以看出,转动惯量矩阵是实对称矩阵,由矩阵理论可知,存在正交矩阵 
![]() ,使得转动惯量矩阵实现对角化,如下所示。
,使得转动惯量矩阵实现对角化,如下所示。
| (5) |
由此可根据变换矩阵 
![]() 建立轮盘的惯性主坐标系,即可使惯性矩阵对角化的随体坐标系,如图4所示,惯性主坐标系以质心为原点,坐标轴称作惯性主轴,与转子自转方向平行的坐标轴一般称为极惯性主轴,另两个坐标轴称作直径惯性主轴,对应极转动惯量
建立轮盘的惯性主坐标系,即可使惯性矩阵对角化的随体坐标系,如图4所示,惯性主坐标系以质心为原点,坐标轴称作惯性主轴,与转子自转方向平行的坐标轴一般称为极惯性主轴,另两个坐标轴称作直径惯性主轴,对应极转动惯量 
![]() 与直径转动惯量
与直径转动惯量 
![]() 。
。

图4 惯性主坐标系示意图Fig.4 Schematic diagram of principal coordinate system of inertia
因此,可采用质心和惯性主轴的空间位置完整描述轮盘的质量分布特性,根据其与旋转中心线(两侧支点连线)的相对关系,质量分布特性可以分为三类:质心偏移、惯性主轴倾斜和惯性主轴偏斜。其中,质心偏移(如图5(a))是指质心G偏离旋转中心线,质心G与形心C之间的距离为e,但极惯性主轴仍平行于旋转中心线;惯性主轴倾斜(如图5(b))是指轮盘惯性主轴与旋转中心线存在夹角τ,质心G仍位于旋转中心线之上;惯性主轴偏斜(如图5(c))则是同时存在质心偏移和惯性主轴倾斜,并且两者存在一定的相位差,这是※具有普适性的质量分布特性,也是工程中※常见的分布特性。

图5 轮盘质量分布示意图Fig.5 Schematic diagram of mass distribution of disk
在工程应用中,描述轮盘质量分布时,不能仅仅采用质心偏移的描述方法,还应同时考虑惯性主轴的倾斜,从而完整描述轮盘质量分布特性。进一步可通过质心和惯性主轴的空间位置,完整描述轮盘的旋转惯性。下面分别推导由质心和惯性主轴的非惯性运动产生的旋转惯性载荷。
2.2 横向旋转惯性载荷
轮盘旋转时,质心做横向非惯性运动,轮盘将受到横向惯性载荷作用。如图6所示,为轮盘涡动时质心的运动示意图, 
![]() 为旋转中心线的投影点,
为旋转中心线的投影点, 
![]() 为转子进动角,
为转子进动角, 
![]() 为自转角。
为自转角。

图6 轮盘质心运动示意图Fig.6 Schematic diagram of motion of the center of mass轮盘横向运动产生的旋转惯性载荷为
| (6) |
将质心运动分解为轮盘形心C与偏心位矢 
![]() 的矢量和
的矢量和
| (7) |
偏心位矢 
![]() 可写作复数形式
可写作复数形式
| (8) |
可得横向旋转惯性载荷的完整表达式
| (9) |
其中 
![]() 为自转角,
为自转角, 
![]() 为自转角速度。以稳态圆进动为例,进动转速为
为自转角速度。以稳态圆进动为例,进动转速为 
![]() ,
, 
![]() ,
, 
![]() 为进动角与自转角的相位差,式(9)可化为
为进动角与自转角的相位差,式(9)可化为
| (10) |
式中第一项通常称为离心载荷,第二项通常称为不平衡载荷。
2.3 角向旋转惯性载荷
转子轮盘旋转时,不仅质心做非惯性运动,惯性主轴的角向非惯性运动,也会使轮盘受到角向惯性载荷作用。如图7所示,为轮盘涡动时惯性主轴的运动示意图, 
![]() 为轮盘质心,
为轮盘质心, ![]() 为绝※坐标系,
为绝※坐标系, ![]() 各坐标轴平行于
各坐标轴平行于 ![]() ,原点位于轮盘质心,
,原点位于轮盘质心, ![]() 为固定于轮盘上的质心坐标系,
为固定于轮盘上的质心坐标系, 
![]() 始终沿自转轴方向,
始终沿自转轴方向, ![]() 为轮盘的惯性主坐标系。轮盘质量分布不均匀时,惯性主坐标系与形心轴坐标系不重合,设
为轮盘的惯性主坐标系。轮盘质量分布不均匀时,惯性主坐标系与形心轴坐标系不重合,设 ![]() 与
与 ![]() 夹角为
夹角为 
![]() ,也即轮盘质量分布不均所致的惯性主轴倾斜角[18⁃19]。
,也即轮盘质量分布不均所致的惯性主轴倾斜角[18⁃19]。

图7 轮盘坐标系示意图
Fig.7 Schematic diagram of coordinate systems of disk
设 ![]() 与
与 ![]() 夹角为
夹角为 
![]() ,
, ![]() 与
与 ![]() 夹角为
夹角为 ![]() ,
, ![]() 与
与 ![]() 夹角为
夹角为 
![]() ,
, ![]() 与
与 ![]() 夹角为
夹角为 ![]() ,
, ![]() 与
与 ![]() 夹角为
夹角为 ![]() ,绝坐标系中,轮盘的角动量可写作
,绝坐标系中,轮盘的角动量可写作
| (11) |
与横向旋转惯性载荷相类似,将惯性主坐标系与形心轴坐标系建立关联
| (12) |
引入复数写法 
![]() ,角向旋转惯性载荷的完整表达式可写作
,角向旋转惯性载荷的完整表达式可写作
| (13) |
以稳态圆进动为例,涡动的角向位移如下:
| (14) |
角向旋转惯性载荷可化简为
| (15) |
第一项通常称为陀螺力矩,是由轮盘涡动所产生的阻抗力矩,第二项则是由转子质量分布不均所产生的惯性力矩激励。
2.4 物理内涵
综上,稳态圆进动状态下,轮盘旋转惯性载荷的完整表达式为
| (16) |
按照旋转惯性载荷的产生机理,可将其分为初始旋转惯性载荷 ![]() 和
和 ![]() ,是由转子加工/装配等初始误差引起的质量分布不均匀所致,如图8(a)所示;以及附加旋转惯性载荷
,是由转子加工/装配等初始误差引起的质量分布不均匀所致,如图8(a)所示;以及附加旋转惯性载荷 
![]() 和
和 
![]() ,由转子进动(包括横向与角向)所产生,如图8(b)所示。
,由转子进动(包括横向与角向)所产生,如图8(b)所示。

图8 轮盘旋转惯性载荷的产生机理示意图Fig.8 Schematic diagram of generation mechanism of rotary inertial load
3 局部旋转惯性⁃连续转轴系统模型
随着高速转子系统的“盘⁃轴角向位移非连续性”逐步显著,轮盘局部运动独立于转轴横向运动。因此,需要提出考虑轮盘局部旋转惯性的转子系统模型及运动方程,以准确描述上述非连续转子系统的动力特性。如图9所示,为典型航空燃气轮机转子系统示意图,轮盘两侧存在连接结构,实现与转轴的连接。对于此类非连续转子系统而言,转轴等连续结构处仍可基于各种梁理论,仅考虑横向二维运动,而轮盘局部则应考虑其四维运动(横向二维与角向二维),连接结构与几何突变处可等效为局部弹簧,从而进一步分析轮盘局部四维旋转运动对转子系统二维运动的“降维影响”。

图9 典型航空燃气轮机转子系统结构示意图Fig.9 Schematic diagram of typical structure of aero⁃engine rotor system
3.1 力学模型
因此,本文提出了局部旋转惯性⁃连续转轴系统模型,如图10所示,由均匀连续轴段、刚性轮盘、盘⁃轴之间的局部弹簧组成。

图10 非连续转子示意图Fig.10 Schematic diagram of non⁃continuous rotor model非连续转子的自由度定义如下,转轴的横向自由度为 
![]() 和
和 
![]() ,轮盘形心的横向自由度为
,轮盘形心的横向自由度为 
![]() 和
和 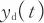
![]() ,轮盘形心轴的角向自由度为
,轮盘形心轴的角向自由度为 
![]() 和
和 
![]() ,并采用复数写法,如下:
,并采用复数写法,如下:
| (17) |
非连续性体现在,盘⁃轴角向位移不相等
| (18) |
式中 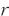
![]() 是转轴横向位移,
是转轴横向位移, 
![]() 是轮盘横向位移,
是轮盘横向位移, 
![]() 是轮盘角向位移,均是复数。此处以等截面欧拉梁为例,密度为
是轮盘角向位移,均是复数。此处以等截面欧拉梁为例,密度为 
![]() ,截面积为A,弹性模量为E,截面惯性积为I,跨度为
,截面积为A,弹性模量为E,截面惯性积为I,跨度为 
![]() ,轮盘位于
,轮盘位于 
![]() 处。为模拟盘⁃轴之间连接结构的刚度特性,可采用线性刚度模型,并假设盘⁃轴之间的弹性力仅与盘⁃轴位移差有关,刚度矩阵为
处。为模拟盘⁃轴之间连接结构的刚度特性,可采用线性刚度模型,并假设盘⁃轴之间的弹性力仅与盘⁃轴位移差有关,刚度矩阵为
| (19) |
式中 ![]() 是盘⁃轴之间的相对横向刚度,
是盘⁃轴之间的相对横向刚度, ![]() 是盘⁃轴之间的相对角向刚度,
是盘⁃轴之间的相对角向刚度, ![]() 是盘⁃轴的横向与角向自由度的耦合刚度。
是盘⁃轴的横向与角向自由度的耦合刚度。
3.2 运动微分方程
以下利用Hamilton原理建立运动微分方程
| (20) |
式中 ![]() 为变分符号,
为变分符号, ![]() 为系统动能,
为系统动能, ![]() 为系统势能,
为系统势能, ![]() 、
、 ![]() 为某一时间段,
为某一时间段, 
![]() 为时间。推导过程较为复杂,此处直接给出结果。
为时间。推导过程较为复杂,此处直接给出结果。
| (21) |
式中 
![]() 为单位脉冲函数。从式(21)可以看出,后两个方程与刚性转子的“四自由度模型”相似,刻画的是轮盘的横向与角向旋转运动,第一个方程则是描述局部旋转惯性影响下连续转轴的横向运动。轮盘旋转惯性载荷通过影响盘⁃轴连接点的横向与角向位移,从而改变转子系统动力学特性。随着轮盘所受的旋转惯性载荷不断增大,轮盘与转轴之间的变形差逐步增大,此时如果单独采用“四自由度转子”模型还是“梁模型”,都无法准确刻画轮盘⁃转轴系统的动力学响应,会导致物理本质不清、影响规律不明、仿真精度不高等问题。
为单位脉冲函数。从式(21)可以看出,后两个方程与刚性转子的“四自由度模型”相似,刻画的是轮盘的横向与角向旋转运动,第一个方程则是描述局部旋转惯性影响下连续转轴的横向运动。轮盘旋转惯性载荷通过影响盘⁃轴连接点的横向与角向位移,从而改变转子系统动力学特性。随着轮盘所受的旋转惯性载荷不断增大,轮盘与转轴之间的变形差逐步增大,此时如果单独采用“四自由度转子”模型还是“梁模型”,都无法准确刻画轮盘⁃转轴系统的动力学响应,会导致物理本质不清、影响规律不明、仿真精度不高等问题。
3.3 主要影响参数
影响局部旋转惯性⁃转轴系统动力特性的主要影响因素有两个:盘⁃轴连接局部刚度、轮盘极/直径转动惯量比。盘⁃轴连接局部刚度直接决定轮盘旋转惯性对转轴动力特性的影响程度。在真实转子结构设计中,有时会采用折返式、发卡式结构以降低局部角向刚度 
![]() 和耦合刚度
和耦合刚度 
![]() ,从而使转子动力特性满足设计要求。考虑到转子结构变化时,通常导致角向刚度与耦合刚度的同步变化,后续仿真中,改变角向刚度时,以相同的比例改变耦合刚度。轮盘极/径转动惯量比,也是影响轮盘旋转惯性的另一关键因素,其定义为三维结构体的极转动惯量与直径转动惯量之比,体现了转子质量的空间分布特征,薄盘(如单级涡轮转子)的转动惯量比接近于2,多级轮盘(如轴流压气机转子组件)的转动惯量比通常小于1。正进动状态下,极转动惯量引起的旋转惯性将加强转子刚性,直径转动惯量引起的旋转惯性则削弱转子刚性,极/径转动惯量比决定了轮盘旋转惯性的综合作用效果,薄盘与多级轮盘的旋转惯性具有明显的不同。
,从而使转子动力特性满足设计要求。考虑到转子结构变化时,通常导致角向刚度与耦合刚度的同步变化,后续仿真中,改变角向刚度时,以相同的比例改变耦合刚度。轮盘极/径转动惯量比,也是影响轮盘旋转惯性的另一关键因素,其定义为三维结构体的极转动惯量与直径转动惯量之比,体现了转子质量的空间分布特征,薄盘(如单级涡轮转子)的转动惯量比接近于2,多级轮盘(如轴流压气机转子组件)的转动惯量比通常小于1。正进动状态下,极转动惯量引起的旋转惯性将加强转子刚性,直径转动惯量引起的旋转惯性则削弱转子刚性,极/径转动惯量比决定了轮盘旋转惯性的综合作用效果,薄盘与多级轮盘的旋转惯性具有明显的不同。
4 局部旋转惯性下转子动力特性
以薄盘⁃连续转轴系统为例,剖析轮盘局部旋转惯性载荷对转子系统动力特性的影响规律。算例参数如表1所示。
表1 算例转子系统参数Table 1 Parameters of rotor system case

需要说明的是,本文图中的“转速比”和“无量纲化模态频率”均以第1阶模态频率进行归一化的,“当量支点动载荷”是以第1阶临界转速的支点反力进行归一化的。
4.1 模态特性
表1所示的薄盘⁃连续转轴系统Campbell图,如图11所示,图中绘出了前3阶正进动模态,振型如图12所示,从中可以看出,各阶模态频率随转子自转转速不断提高,这是由于转子系统模态主要由转轴弯曲变形所决定,并受轮盘局部旋转惯性的影响。由于盘⁃轴局部连接刚度的存在,当轮盘产生角向位移时,轮盘的附加角向旋转惯性载荷,也即陀螺力矩,正进动状态下,将对转轴横向变形起到抑制作用,等效增强转轴弯曲刚度,使得转子正进动模态频率提高。

图11 典型薄盘⁃连续转轴系统的Campbell图Fig.11 Campbell diagram of typical disk⁃continuous rotor shaft system
图12 前3阶模态振型图
Fig.12 Modal shapes of the first three modes
在图11算例的基础上,只降低盘⁃轴连接角向刚度,可得到转子第1阶模态频率的变化规律,如图13所示。从图中可用看出,随着盘⁃轴连接角向刚度的降低,轮盘旋转惯性对转轴弯曲刚度的增强作用减弱,体现为转子弯曲模态频率增幅的不断减少,※为明显的是当角向刚度为1×106 
![]() 时,模态频率线的增幅近似为零,即盘‑轴连接刚度较弱时,轮盘旋转惯性对转子动力特性的影响程度大幅降低。
时,模态频率线的增幅近似为零,即盘‑轴连接刚度较弱时,轮盘旋转惯性对转子动力特性的影响程度大幅降低。

图13 局部角向刚度对转子模态频率的影响Fig.13 Influence of local angular stiffness on the modal frequency of rotor
4.2 振动响应
在掌握轮盘⁃连续转轴系统模态特性的基础上,继续分析轮盘质量分布不均匀情况下,转子系统的强迫振动响应。以图5所示的质量分布特性分类为基础,着重讨论不同质量分布对转子系统动力学响应的影响。本文以第1阶弯曲模态为例,探究轮盘旋转惯性载荷对转轴弯曲振动的影响,为减少高阶模态的影响,不妨适当降低转轴密度,将高阶弯曲模态频率提高至本文研究的转速范围以外。4.2.1 质心偏移激励质心偏移,即轮盘仅存在质心偏移,而无惯性主轴倾斜,令式(21)中,偏心距 
![]() ,初始倾斜角
,初始倾斜角 
![]() ,求解薄盘⁃连续转轴系统动力学响应,如图14所示。
,求解薄盘⁃连续转轴系统动力学响应,如图14所示。

图14 质心偏移激励下薄盘⁃连续转轴系统动力学响应Fig.14 Dynamic response of the thin disk⁃continuous shaft system under unbalance从图14中可以看出,在转速比为1~7的范围内,轮盘与转轴的曲线几乎重合,横向位移差近似为零,即盘⁃轴横向位移的非连续性较小。因此,这一转速范围内,薄盘⁃连续转轴系统的动力学响应与“Jeffcott转子”相同,在超临界状态下,发生“质心转向”,并逐渐自动定心,振动幅值趋近于偏心距,示意图如图15所示。

图15 轮盘质心自动定心示意图Fig.15 Schematic diagram of self⁃centering phenomenon of center of mass4.2.2 惯性主轴倾斜激励为准确、完整描述轮盘质量分布特性,除常见的质心偏移之外,还必须考虑惯性主轴倾斜,及其旋转惯性激励下转子系统的动力学响应。令式(21)中偏心距 
![]() ,初始倾斜τ=3×10-4 rad,求解薄盘⁃连续转轴系统动力学响应,如图16所示。
,初始倾斜τ=3×10-4 rad,求解薄盘⁃连续转轴系统动力学响应,如图16所示。

图16 惯性主轴倾斜激励下薄盘⁃连续转轴系统振动响应
Fig.16 Vibational response of thin disk⁃continuous shaft system under skew unbalance
从图16中可以看出,与质心偏移激励不同,在惯性主轴倾斜激励下,轮盘与转轴并无通过临界转速后振动持续降低的特征,相反,超临界状态下(转速比为1~140),转子角向变形随转速提高而不断增加。随着转速继续提高(转速比为1~140),轮盘与转轴之间的“角向位移非连续性”不断增大,轮盘与转轴振幅变化逐渐趋缓,轮盘角向位移逐渐趋近于初始倾斜角。上述现象的内在机理与“质心转向”相同,在轮盘绕旋转中心线高速旋转时,倾斜的惯性主轴具有自动掰正的趋向,这是由其自身旋转惯性所决定的,示意图如图17所示。在除临界转速附近之外的宽广转速范围内,轮盘角向位移与初始倾斜角的相位差始终为180°,即轮盘在其旋转惯性载荷作用下,始终朝着减小惯性主轴倾斜量的方向进行旋转运动,在较高转速下,轮盘惯性主轴近

图17 轮盘惯性主轴定心示意图Fig.17 Schematic diagram of self⁃centering phenomenon of principal axis of inertia似重合于旋转中心线,实现了“惯性主轴掰正”,由此引起的转轴弯曲变形逐步增大,进而导致转子支点动载荷不断增大。4.2.3 惯性主轴偏斜激励工程应用中,无论是航空燃气轮机还是地面燃气轮机,其高速转子系统,尤其是多盘堆叠而成的轮盘组件,一般均处于动不平衡状态下,此时轮盘同时存在质心偏移和惯性主轴倾斜,受到初始旋转惯性载荷作用。如图18所示,为典型航空燃气轮机高压转子的典型动力学响应图,质心偏移引起的振幅在临界转速处存在局部峰值,惯性主轴倾斜引起的振幅则随转速升高而持续增大,导致转子系统动力学响应体现出“振幅随转速升高而不断增大,在临界转速处存在局部峰值”的特征。

图18 典型航空燃气轮机高压转子动力学响应Fig.18 Typical dynamic response of high pressure
rotor of aircraft gas turbine engine4.2.4 局部角向刚度的影响盘⁃轴连接局部角向刚度的降低,对转子动力学响应的影响也十分显著,此处仍以文中第4.2.2节中的惯性主轴倾斜激励为例。选取角向刚度为 
![]() 和
和 
![]() ,绘制转子盘⁃轴角向变形情况,如图19所示。对比图16(a)(角向刚度为
,绘制转子盘⁃轴角向变形情况,如图19所示。对比图16(a)(角向刚度为 
![]() )可知,通过提高盘⁃轴连接局部角向刚度,可以有效提高盘‑轴角向位移的连续性,在相同转速下,轮盘与该处转轴的角向位移差较小。
)可知,通过提高盘⁃轴连接局部角向刚度,可以有效提高盘‑轴角向位移的连续性,在相同转速下,轮盘与该处转轴的角向位移差较小。

图19 不同局部角向刚度下转子角向变形
Fig.19 Angular displacement of rotor under different local angular stiffness
但盘⁃轴连接角向刚度的提高,也将导致轮盘旋转惯性对转轴振动的影响程度明显提高,支点动载荷明显增大,如图20所示。相反,降低盘⁃轴连接局部角向刚度,可降低转子支点动载荷,有利于旋转机械的可靠运转。这一规律可用于先进航空燃气轮机转子动力学设计,且在国内外某些先进型号中已有应用。

图20 不同局部角向刚度下的转子支点动载荷Fig.20 Bearing dynamic load of rotor under different local angular stiffness
5 结 论
本文针对盘⁃轴“角向位移非连续”转子系统,研究了轮盘局部旋转惯性对转子动力特性的影响机理和规律,总结如下:1) 提出了基于质心和惯性主轴的转子旋转惯性的准确描述方法,并通过理论推导证明了此方法的完备性。从惯性载荷的一般性定义出发,推导了由转子质心偏移和惯性主轴倾斜产生的旋转惯性载荷表达式,并分析了物理内涵;2) 在旋转惯性模型的基础上,提出了具有局部旋转惯性的连续转轴转子模型,并建立了运动微分方程组,揭示了轮盘局部旋转惯性对转子动力学响应的影响机理;3) 在传统转子动力学“超临界状态下质心自动定心”概念的基础上,提出了“高转速下惯性主轴自动掰正”的概念,丰富了转子旋转惯性的物理内涵,并解释了高转速下转子支点动载荷随转速提高而持续增大的力学过程;4) 以工程中常见的质心偏移、惯性主轴倾斜激励为例,分析了局部旋转惯性载荷下的转子动力特性,探究了盘⁃轴局部连接刚度的影响规律,对理解工程中的转子振动现象、分析振动问题,以及开展转子动力学设计,具有一定的参考价值。
局部旋转惯性对转子系统动力特性的影响
洪杰 杨哲夫 孙博 宋制宏 马艳红
北京航空航天大学 能源与动力工程学院
北京航空航天大学 航空发动机研究院
中国航空发动机集团有限公司 沈阳发动机研究所
DOI:10.13224/(暂不可见)ki.jasp.20210579
引用本文:洪杰,杨哲夫,孙博,等.局部旋转惯性对转子系统动力特性的影响[J].航空动力学报,2022,37(4):673‑683. (HONG Jie,YANG Zhefu,SUN Bo,et al.Influence of local rotary inertia on the dynamic properties of
rotor systems[J].Journal of Aerospace Power,2022,37(4):673‑683.)
作者简介:洪杰(1965-),男,教授、博士生导师,博士,从事航空燃气轮机转子动力学、整机动力学研究。
(航空动力学报)
声明:本网站所收集的部分公开资料来源于互联网,转载的目的在于传递更多信息及用于网络分享,并不代表本站赞同其观点和对其真实性负责,也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传,对此类作品本站仅提供交流平台,不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题,请第一时间告知,我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容,以保证您的权益!联系电话:010-58612588 或 Email:editor@mmsonline.com.cn。

- 暂无反馈










