船舶电力系统的振动及其控制仿真研究

0 引言

船舶系统在航行过程中随时会遇上风浪，风浪将不可避免的对整个传播系统造成振动。而振动是造成船舶电力系统受到严重损坏的灾害之一。船舶在航行中强烈的振动会使得电气设备发生短路故障或基础松动破坏，而且会造成整个电力设施的瘫痪或崩溃。电力系统的破坏还将导致众多其他的灾难：船员正常的生产、生活无法开展，如遇突发事件（火灾、缺水）等，将造成不可预计的严重后果。

根据国内外电气系统在船舶应用中因为振动失效情况来看，电气系统失效危害集中在以下方面：(1)变压器的破坏：由于强力的振动，使得固定在传播上的螺栓因为剪力而发生折断或者在振动中没有良好的防松装置等方式的失效，造成变压器的损毁；(2)蓄电池的破坏：蓄电池在船舶中扮演很重要的角色，一旦其发生破坏很多备用装置无法启动，将造成整个船只的混乱，后果不堪设想；(3)互感器的破坏：电压互感器、电流互感在强力的振动中会从没有固定好的支架上跌落，这将导致瓷件的破碎或者线路折断等故障的发生。此外，由于地震使电流互感器处于开路状态，这就可能产生高电压短路造成设备或线路被烧毁等次生灾害。

因此，为了避免上述各类危害在船舶运行中发生，开展关于振动对于船舶电力系统的破坏的研究就十分有必要，本文基于振动实验的基础上分析各类振动对于电力系统的影响，找出对船舶电力系统振动较小的固定方式方法。同时也为后续进一步研究提供必要的实验依据。

1 振动实验

1.1 实验方法

为了对整个船舶电力系统的模拟分析，需要对各电气设施的各个部分进行模态分析，这有利于了解它们的动力各项特征，为后续的振动实验提供必要的理论依据。本实验中主要是经过振动实验后进行数据的测定，因此将采用时程分析法进行分析。该方法是把动力以时间函数的方式导入微分方程中，并通过积分的方法得到各时刻的响应及其变化情况。

结合船舶电力系统以及相应结构特点，本文采用积分法中的HHT法对配电系统的振动反应进行分析。基于HHT法是将系数α引入并修改相应的结构动力方程，如公式（1-1），对该公式使用Newmark方法进行计算求解。

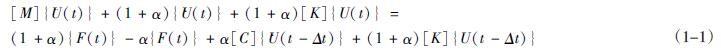
上式中α=0-0.3区间。

使用泰勒公式展开，则

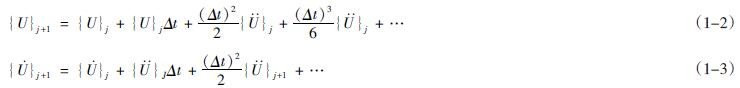
对于上式进行积分则可以得到：

将（1-4）分别带入（1-1）和（1-2）则可得：

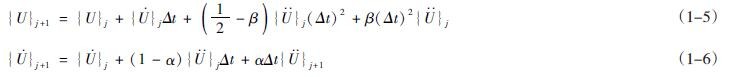
上述所有计算公式中都是基于在单位时间步长（Δt）内的刚度、阻尼、振动，输入加速度，它们均不发生变化。

1.2 实验材料

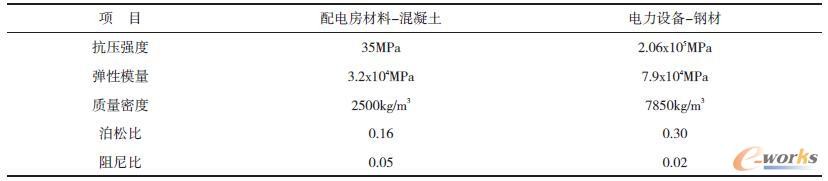
在船舶电力系统中，一般均有单独的配电房间。本实验为了模拟出船舶在实际航行中的状况，分别作了以下假设：配电房材料采用混凝土结构来保持其坚固性，而电力设备均采用钢材。两种材料的主要参数对比表如表1所示。

表1 两种材料主要参数对比

1.3 振动类型的定义

为了模拟各种波动下对于电力系统的影响，分别选择了不同的场地类型的振动波来进行对比实验，这也会使得所获得的电力系统的分析结果更具有普遍意义。各种类型的振动输入如表2所示。

表2 振动实验的振动波列表

1.4 质量比定义

为了显示单位电气质量在所放置质量中的振动效果，定义质量比概念如下：

上式中β为电气设备总质量与配电房的整体的质量之比，me和ms分别是电气设备总质量和配电房质量。

2 振动结果分析

2.1 不同质量比和场地类型位移影响分析

表3为设备处于不同质量比在不同工况水平下的最大位移分析。

表3 设备处于不同质量比的不同工况下最大位移分析

从表3可以看出：①随着设备质量比的增大，设备的振动输出效果则表现得越发强烈，这个趋势可以从图1看出。②从图2可以看出在不同的类型场地上即使同样的设备质量比也会出现不同的位移分布状态，由图可以看出I类的场地总体来说是位移最小的，而IV类场地则出现最大的位移幅度，II、III类介于两则之间。因此在电力设备的布置当中如果能够选择I类场地则能够有效降低其位移量，在实际运用中尽力避免IV场地的布置。

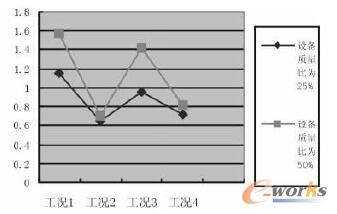
图1 I类场地不同设备质量比位移图

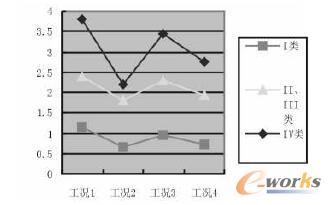
图2 不同类场地位移分布图

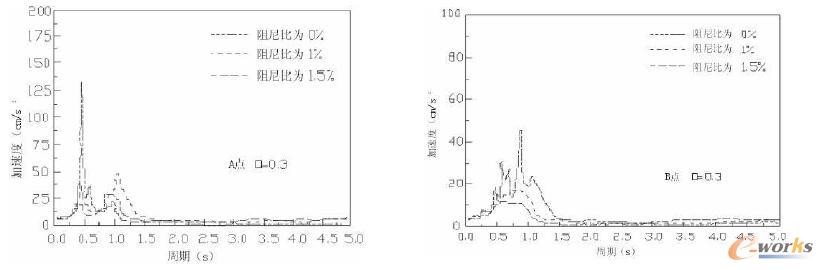
图3 质量比为0.3下的A、B点在不同阻尼比条件下的加速度对比

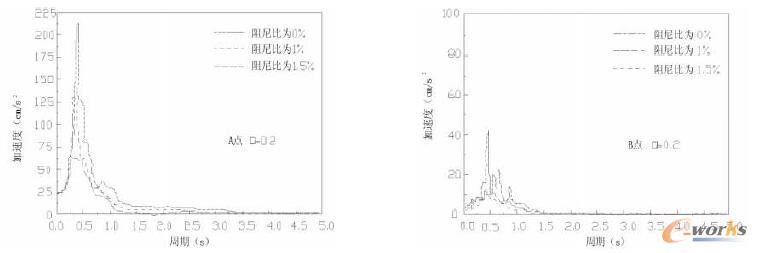
图4 质量比为0.2下的A、B点在不同阻尼比条件下的加速度对比

2.2 电气系统在振动中的加速度谱分析

图3和图4分别为不同质量比的电气设备经受振动波峰值加速度为400cm/s²作用下，电气设备上所取A点及该点所在配电房地板B点取其阻尼分别为0%，1%以及1.5%条件下的加速度频谱对比图。

通过对比上述两图中可以得到以下结果：

(1)通过观察图3和图4可以看到不管是何种质量比的设备，A点的频谱都比B点的频谱频带更加狭窄，A点频谱的振动的峰值都比B点要高，且更为集中，说明该部分集中了主要的能量。而实验A点为电气设备上的点，这说明其具有更高的能量，也就将获得更大的加速度，这在振动中也就更具破坏力；而B点为配电房所在地板上的点，其在收到冲击时所受到的冲击则相对A点来说小了很多。

(2)观察图3和图4的不同阻尼比下的频谱曲线可以看出，各个频谱的形状接近，但是随着阻尼的变化出现一定的差异。从其形状接近知道本次实验基本接近于真实的冲击振动试验，而不同阻尼比则反映了不同的阻力对于设备抗振动性能有直接联系：阻尼比大的其振动峰值较小，阻尼比小的其频谱峰值较大。因此，在设计过程中要增加设备的阻尼比。

(3)图3所示为设备质量比β=0.3时的频谱，从图上可以看出A点的频谱峰值出现在的周期约为对应的周期为0.45s，而B点频谱峰值出现在的周期约为对应的周期为0.82s。这就反映出电气设备的频谱峰值同配电房对应的峰值是错开的，在该工况下电气设备的振动周期能够有效地避开了配电房的振动周期，二者不会发生共振现象，这就能够减少电气设备的振动。反观图4所示设备质量比β=0.2时的频谱，A点和B点的频谱峰值出现在的周期均在0.5s附近，在该状态下就有可能形成电气设备同配电房形成共振现象，这将会明显放大电气设备的振动频谱，造成设备的强力振动。

3 船舶电力系统振动破坏仿真分析

3.1 仿真过程

为了对船舶电力系统的抗振性能进行分析，建立了仿真模型如图5所示。使用仿真对系统进行模拟并进行计算分析，这样能够在设计过程中就对系统进行改进，提高效率。本次模拟实验以船舶正在运行时遭遇大的波浪形成强震动，使用上述的IV类场地1型工况，为Tri型振动波。整个过程如下：首先是发电机组正常启动并组网运行，之后液压油泵启动，经过0.1s后两翼推进器启动运行，0.2s时液压泵的电路发生接地故障，0.4s时由于电路中的短路电流过大发动机组自动跳闸保护。

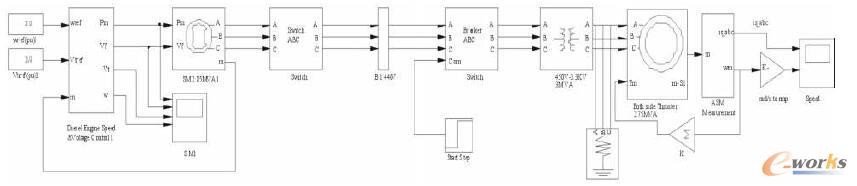
图5 系统仿真模型

3.2 结果分析

(1)两翼推进器启动时电流和转速的变化。该失效状态如下所述：0.1s时由于两翼推进器的启动，因此起动电流将会变得更大。0.2s时侧推器的起动电流将减小。受到振动发生接地故障0.4s时发电机跳闸保护，则起动电流为0，转速开始下降，参数变化如图6所示。

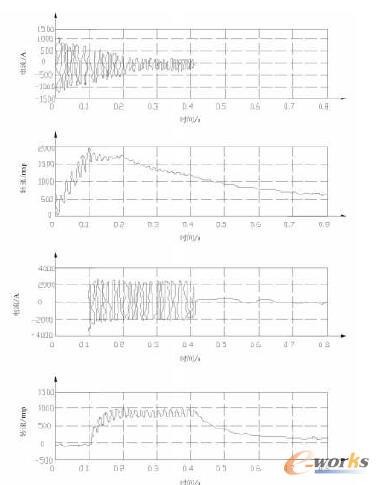
图6 液压泵以及两翼推动器短路后电流及转速图

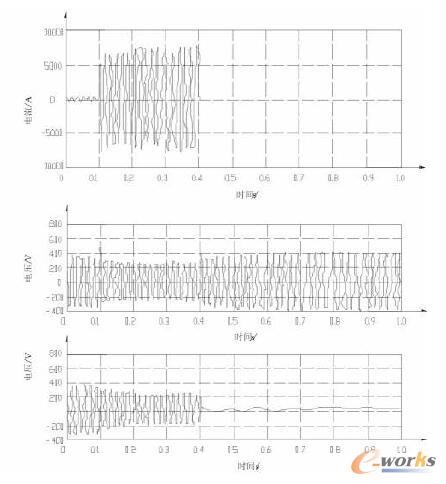
图7 短路后发电机组电流、电压及电网电压

(2)发电机组电流、电压和电网相电压变化。该失效状态如下所述：液压泵(220kW)起动时，由于初始外界负载比较小，发电机输出电流也相对较小。0.1s时两翼推进器(2300kW)起动，由于该项负载很大，发电机输出将出现电流高峰值。之后遭遇振动，0.2s时发生三相接地故障，使发电机的电流达到极限值，0.4s时发电机组跳闸保护，输出电流为零。对于电压来说，包含外加载荷状态下电压不可避免要出现下降，在接地故障发生时输出电压下降到极限值，在开关跳闸保护后电网的电压为零，电网失压，参数变化如图7的电流以及电压所示。

4 结论

船舶系统在行驶过程中会出现很多的颠簸，因此其内部系统的抗振动能力至关重要。对于其电力系统的抗振动能力需要进行测试，并找出最优的抗振动方法。文章通过使用多种模拟船舶电气柜或配电房，采用不同的质量比对不同的振动输入进行测试，并对结果进行了分析，获得了以下结论：(1)在同一工况下设备质量比对电气设备的振动有直接的影响；质量比越大则设备的振动越强烈；(2)场地类型对振动位移有影响，在实际运用中尽力避免IV场地的布置；(3)不同阻尼比下的频谱曲线能够反映真实的冲击振动，阻尼比小的其频谱峰值较大。因此，在设计过程中要增加设备的阻尼比；(4)设备质量比不同将会形成不同的电力系统和配电柜的频谱，在实际运行过程中要尽力避免二者频谱的重叠，尽力减少电力系统和配电柜的共振，以期减轻对电力系统的振动，保护船舶电力设备；(5)通过对振动破坏下系统短路进行模拟分析，指出振动破坏对于电力系统的影响。

（互联网 作者：庄一凡 ）

声明：本网站所收集的部分公开资料来源于互联网，转载的目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传，对此类作品本站仅提供交流平台，不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题，请第一时间告知，我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容，以保证您的权益！联系电话：010-58612588 或 Email:editor@mmsonline.com.cn。