轴向载荷对载荷分布的影响

　　当向心推力轴承承受径向载荷R时，由于滚动体与滚道的接触线与轴承轴线之间夹一个接触角α，因而各滚动体的反力Ni并不指向半径方向，而是沿接触点的法线方向，它可以分解为一个径向分力和一个轴向分力。用Pi代表某一滚动体反力的径向分力，则相应的轴向分力Fdi应等于Pi tgα。所有径向分力Pi的合力R’与径向载荷R相平衡；所有的轴向分力Fdi之和组成轴承的派生轴向力Fd，它迫使轴颈（连同轴承内圈和滚动体）向右移动，并最后与轴向力Fa平衡。
　　当只有一个滚动体受载时，即载荷角和接触角相等。

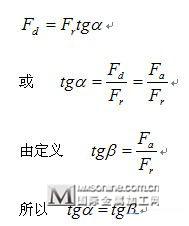
　　当受载的滚动体数目增多，虽然在同样的径向载荷Fr的作用下，但派生的轴向力Fd将增大。因这时作用于各滚动体上的径向反力Pi的方向各不相同，它们的向量和R’虽然与Fr平衡，但其代数和必大于Fr，而派生的轴向力Fd是由各个Pi分别派生的轴向力Fdi合成的，其值应按Fdi的代数和计得。所以在同样的径向载荷Fr作用下，由作用于各滚动体上Pi的分别派生的轴向力所合成的轴向力Fd，将比只有一个滚动体受载时派生的轴向力大。即

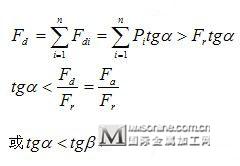
　　以上分析说明：

　　1）向心推力轴承必须在径向载荷R和轴向力A的联合作用下工作。

　　2）对于同一轴承，在同样的径向载荷R作用下，当受载的滚动体数目不同时，就派生出不同的轴向力S，也就需要不同的轴向力A来平衡它。或者反过来说，在径向载荷R不变的条件下，当轴向力由最小值（Fa=Frtgα，这时由一个滚动体受载）逐步增大（即β角增大），这意味着轴承内接触的滚动体数目逐渐增多。

　　对实际工作的向心推力轴承，为保证它能可靠地工作，应使它至少达到下半圈滚动体全部受载。因此，安装这类轴承时，不能有较大的轴向窜动。

声明：本网站所收集的部分公开资料来源于互联网，转载的目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传，对此类作品本站仅提供交流平台，不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题，请第一时间告知，我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容，以保证您的权益！联系电话：010-58612588 或 Email:editor@mmsonline.com.cn。