采用D-K-D迭代算法设计导弹增益调度自动驾驶仪
1 引言(Introduction)
自20世纪90年代以来, 基于H1控制理论的鲁棒 增益调度技术得到了迅速发展, 该技术能够在设计 过程中对系统时变参数进行处理直接生成满足性能 要求的全局线性参数时变(LPV)控制器, 而不需要采 用任何插值运算. 鲁棒增益调度技术具有严谨的理 论基础, 很好地克服了传统增益调度技术局部特性 不能准确反映全局特性, 全局特性只能通过事后的 大量仿真试验进行验证的局限性.
Packard和Apkarian等人的文章给出了求解确定 性LPV系统(不含不可测量不确定性的LPV系统)鲁 棒增益调度问题的方法(以下称为LPV方法). 对于 确定性LPV系统, 可通过求解一个凸优化问题得 到H1增益调度控制器[1s3]. 然而, 在实际应用中被 控LPV系统常常含有不可测量不确定性, 同时在设 计过程中除考虑鲁棒稳定性外还需要考虑系统 的鲁棒性能问题, 由此形成了不确定LPV系统的鲁 棒增益调度问题. 不确定LPV系统的鲁棒增益调度 问题不再是凸优化问题, 不能直接求解. 一种可行的 方法是采用D–K–D迭代算法综合运用LPV控制方法 和¹综合方法进行求解. 与D–K迭代类似, D–K–D迭 代过程不能保证找到全局最优解, 但在实际应用中 非常有效[4;5].
导弹是典型的参数时变系统, 其动力学特性会随 飞行马赫数和高度等参数的变化而大范围变化, 同 时, 制导系统中各种测量器件不可避免地会存在量 测误差和噪声. 因此, 高性能导弹必须通过自动驾驶 仪稳定导弹的动力学特性并抑制量测误差及噪声等 干扰因素造成的不确定性. 本文尝试采用D–K–D迭代算法为地空导弹设计鲁棒增益调度自动驾驶仪.
2 自动驾驶仪LPV/¹设计结构(Autopilot LPV/¹ design structure)
为了应用鲁棒增益调度技术设计导弹自动驾驶 仪, 需要建立导弹的线性分式变换(LFT)模型. 当导 弹动力学特性随攻角变化较小时, 可以基于雅可比 线性化模型建立导弹的LFT模型[6]; 当导弹动力学 特性随攻角变化较大时, 则需要基于准线性化模型 建立导弹的LFT模型[7]. 本文采用了基于雅可比线 性化模型建立的导弹LFT模型, 如图1所示, 模型的 具体建立过程可参见参考文献[6].
图1中, £t为由标一化的导弹飞行马赫数¹M 和高 度¹H 构成的时变参数模块, 具有形式
G(s)为具有2个状态、7个输入和8个输出的线性时不变(LTI)系统, 输入信号u = ±z, 输出信号y = [fy _# ]T, 其中±z为舵偏角, fy为法向加速度, _#为俯仰 角速度. 导弹飞行马赫数M和高度H的变化范围选 取为
为了有效抑制系统中存在的各种不确定性, 并满 足制导回路的性能要求, 自动驾驶仪设计采用了如 图2所示模型匹配设计结构.

自20世纪90年代以来, 基于H1控制理论的鲁棒 增益调度技术得到了迅速发展, 该技术能够在设计 过程中对系统时变参数进行处理直接生成满足性能 要求的全局线性参数时变(LPV)控制器, 而不需要采 用任何插值运算. 鲁棒增益调度技术具有严谨的理 论基础, 很好地克服了传统增益调度技术局部特性 不能准确反映全局特性, 全局特性只能通过事后的 大量仿真试验进行验证的局限性.
Packard和Apkarian等人的文章给出了求解确定 性LPV系统(不含不可测量不确定性的LPV系统)鲁 棒增益调度问题的方法(以下称为LPV方法). 对于 确定性LPV系统, 可通过求解一个凸优化问题得 到H1增益调度控制器[1s3]. 然而, 在实际应用中被 控LPV系统常常含有不可测量不确定性, 同时在设 计过程中除考虑鲁棒稳定性外还需要考虑系统 的鲁棒性能问题, 由此形成了不确定LPV系统的鲁 棒增益调度问题. 不确定LPV系统的鲁棒增益调度 问题不再是凸优化问题, 不能直接求解. 一种可行的 方法是采用D–K–D迭代算法综合运用LPV控制方法 和¹综合方法进行求解. 与D–K迭代类似, D–K–D迭 代过程不能保证找到全局最优解, 但在实际应用中 非常有效[4;5].
导弹是典型的参数时变系统, 其动力学特性会随 飞行马赫数和高度等参数的变化而大范围变化, 同 时, 制导系统中各种测量器件不可避免地会存在量 测误差和噪声. 因此, 高性能导弹必须通过自动驾驶 仪稳定导弹的动力学特性并抑制量测误差及噪声等 干扰因素造成的不确定性. 本文尝试采用D–K–D迭代算法为地空导弹设计鲁棒增益调度自动驾驶仪.
2 自动驾驶仪LPV/¹设计结构(Autopilot LPV/¹ design structure)
为了应用鲁棒增益调度技术设计导弹自动驾驶 仪, 需要建立导弹的线性分式变换(LFT)模型. 当导 弹动力学特性随攻角变化较小时, 可以基于雅可比 线性化模型建立导弹的LFT模型[6]; 当导弹动力学 特性随攻角变化较大时, 则需要基于准线性化模型 建立导弹的LFT模型[7]. 本文采用了基于雅可比线 性化模型建立的导弹LFT模型, 如图1所示, 模型的 具体建立过程可参见参考文献[6].
图1中, £t为由标一化的导弹飞行马赫数¹M 和高 度¹H 构成的时变参数模块, 具有形式
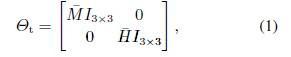
G(s)为具有2个状态、7个输入和8个输出的线性时不变(LTI)系统, 输入信号u = ±z, 输出信号y = [fy _# ]T, 其中±z为舵偏角, fy为法向加速度, _#为俯仰 角速度. 导弹飞行马赫数M和高度H的变化范围选 取为

为了有效抑制系统中存在的各种不确定性, 并满 足制导回路的性能要求, 自动驾驶仪设计采用了如 图2所示模型匹配设计结构.
声明:本网站所收集的部分公开资料来源于互联网,转载的目的在于传递更多信息及用于网络分享,并不代表本站赞同其观点和对其真实性负责,也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传,对此类作品本站仅提供交流平台,不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题,请第一时间告知,我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容,以保证您的权益!联系电话:010-58612588 或 Email:editor@mmsonline.com.cn。

网友评论
匿名:
最新反馈
- 暂无反馈
无须注册,轻松沟通
