虚拟仪器在系统相关辨识中的应用

关键词：相关辨识理论; 虚拟仪器; LABVIEW

Abstract: This paper introduce the application of VI in System Identification . LABVIEW is applied in writing measure-control system.The simulations demonstrate this method is efficient and practical.

Keywords: correlation analysis; VI; LABVIEW

引言

　　控制系统模型的准确性是系统设计的关键问题,直接影响控制精度和运行结果。系统辨识是得到系统模型的一种重要途径。在现代控制工程中,利用伪随机信号结合虚拟仪器技术对系统进行相关辨识,是近年来迅速发展起来的新技术。本文以开发二阶系统参数辨识仪为例，介绍了虚拟仪器在系统参数辨识中的应用方法。

1 系统相关辨识方法

1.1相关辨识基本原理

　　相关辨识的理论基础是Wiener-Hopf方程：

　　（1）

　　（1）式中，Rxx为系统输入的自相关函数，Rxy为系统输入输出的互相关函数，g（t）为系统的脉冲响应函数。根据Wiener-Hopf方程可知，若能取得系统输入的自相关函数Rxx和系统输入输出的互相关函数Rxy,则可以得到系统的脉冲响应函数。但是，对于一般的信号,Wiener-Hopf方程的求解是非常困难得，为此我们要寻找一些特殊的信号作为输入信号以简化求解过程。而白噪声信号其自相关函数具有特殊的形式，其自相关函数为Rxx=K＊δ函数。由此得：

　　（2）

　　可见，系统的输入信号为白噪声时，只要取得系统输入输出的互相关函数Rxy就可求得系统的脉冲响应，见（2）式。但白噪声只是数学上的一个抽象，不容易产生。工程中常使用伪随机信号作为系统的辨识信号。伪随机信号通常采用的是M序列。

1.2 二阶系统参数辨识方法

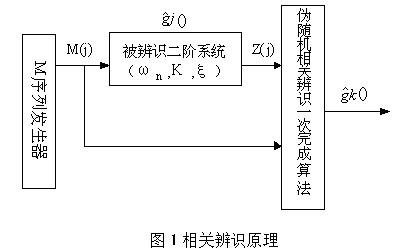
　　系统参数辨识仪以二阶系统为辨识对象。实际应用中，激励信号施加于二阶系统，系统的输出可由数据采集装置获得，并传输至虚拟仪器。本文中，二阶系统模型的特征参数由用户输入确定，二阶系统的输出是由计算得到的。相关辨识原理框图如图（1）所示。

　　M序列发生器所产生的M序列时钟周期?t应该满足如下条件：

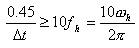　　（3）

　　（3）式中：fh,ωh分别为二阶系统截止频率、截止角频率。该式说明M序列的频带宽度0.45/?t至少要覆盖被辨识系统截止频率fh的10倍以上。M序列的长度N=（1.25～1.5）Ts/?t。其中Ts为系统的调整时间。Ts、fh、ωh可由用户给定的特征参数计算得到。

　　系统的输出是根据系统的模型计算得到的。二阶系统模型的传递函数为：

　　（4）

　　（4）式中：ωn为系统固有角频率,ξ为系统阻尼系数,K为系统比例系数。对（4）式作Z变换可得如下计算公式：

　　（5）

　　（5）式中：M0=4+4ξωnT+ωn2T2,M1=-8+2ωn2T2,M2=4-4ξωnT+ωn2T2,M3=Kωn2T2，T为采样周期。根据（5）式可计算出M序列作为输入时系统的输出。

　　系统脉冲响应的估计值可采用如下的伪随机序列相关辨识一次完成算法：

　　当M序列确定以后，系统的输出z（j）通过计算得出，相应的系统脉冲响应估计值就可由上式计算得出。并且该算法可一次完成N点的脉冲估计值的计算。

2 二阶系统辨识仪的实现

　　采用美国国家仪器公司的图形化编程语言LABVIEW7.1作为系统的编程语言。二阶系统辨识仪的实现分为两个部分：一是仪器虚拟面板的设计;二是后台控制处理程序的设计。

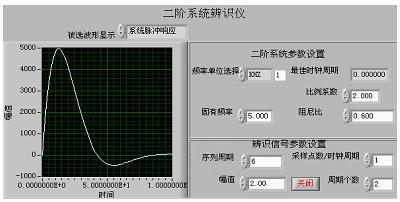
图2 虚拟仪器面板

　　仪器虚拟面板如图（2）所示。虚拟前面板的设计是在Front Panel窗口下，利用LABVIEW的Controls Palette上的各种控件来完成的。面板第一部分是二阶系统参数设置区域。它包含三个数字输入控件numeric control，一个枚举型输入控件enum control和一个数字显示控件numeric indicator。通过这几个控件，我们可以配置二阶系统的参数：比例系数K，系统固有频率fn,系统阻尼系数ξ;第二部分为辨识信号参数设置区域,它包含四个数字输入控件numeric control。在此我们可以设置M序列的幅值、周期、周期个数及仪器的采样时钟周期;第三部分为波形显示区域。它包含一个枚举型输入控件enum control 和一个波形显示控件waveform graph，通过选择，可以显示输入的辨识信号图形、输出信号图形、输入输出互相关图形和系统脉冲响应图形。另外还有一个控制仪器开关的stop button。

　　虚拟辨识仪的后台程序是在LABVIEW的Block Diagram窗口下利用Functions Palette上的控件设计。由于辨识过程要涉及到M序列的发生和一次性相关辨识算法，所以要通过LABVIEW中的MATLAB Script调用MATLAB来完成数据地处理工作。整个图形化程序如图（3）所示，

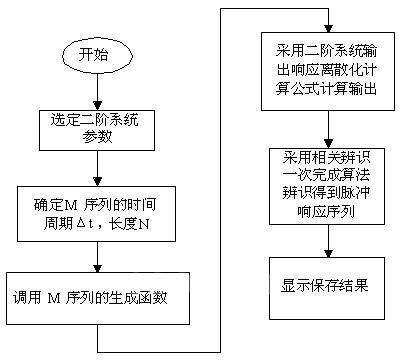
　　其工作流程如图（4）所示。

图4 实验结果

3 实验结果

　　采用二阶系统辨识仪对系统进行辨识，系统模型参数设置为ξ=0.6,K=2,fh=5KHZ,经辨识后得到系统的脉冲响应如图（5）所示。

　　图中实线表示辨识所得系统脉冲响应。虚线表示系统脉冲响应的理论值。由此可见，采用虚拟仪器结合相关辨识法来辨识系统参数具有较高的精度。配合相应的数据采集设备，该辨识仪就能对实际电路参数进行辨识。而且根据系统参数的其它辨识方法（如最小二乘法、极大似然法、随机逼近法等），只要对软件重新设计，就能推广到系统辨识的其他领域。

参考文献：

　　[1]Gary W.Johnson,Richard Jennings 著.《LABVIEW图形编程》[M].北京：北京大学出版社,2002.

　　[2]孙亮主编.《MATLAB语言与控制系统仿真》[M].北京:北京工业大学出版社，2001.

　　[3]李言俊，张科.《系统辨识理论及应用》[M].北京：国防工业出版社，2003.

声明：本网站所收集的部分公开资料来源于互联网，转载的目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。本站部分作品是由网友自主投稿和发布、编辑整理上传，对此类作品本站仅提供交流平台，不为其版权负责。如果您发现网站上所用视频、图片、文字如涉及作品版权问题，请第一时间告知，我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容，以保证您的权益！联系电话：010-58612588 或 Email:editor@mmsonline.com.cn。